Excision is a surgical procedure that involves the complete removal of abnormal tissue, such as tumors or lesions, from the body to prevent further spread or complications. Precise excision techniques minimize damage to surrounding healthy tissues, ensuring better recovery and outcomes. Discover more about how excision can impact your treatment options by reading the full article.
Table of Comparison
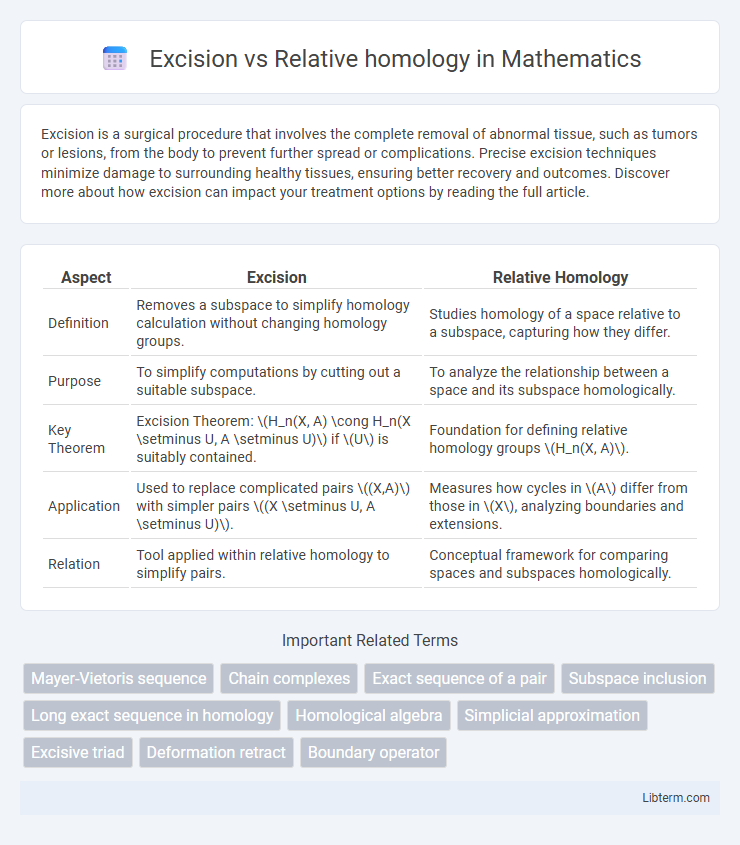
| Aspect | Excision | Relative Homology |
|---|---|---|
| Definition | Removes a subspace to simplify homology calculation without changing homology groups. | Studies homology of a space relative to a subspace, capturing how they differ. |
| Purpose | To simplify computations by cutting out a suitable subspace. | To analyze the relationship between a space and its subspace homologically. |
| Key Theorem | Excision Theorem: \(H_n(X, A) \cong H_n(X \setminus U, A \setminus U)\) if \(U\) is suitably contained. | Foundation for defining relative homology groups \(H_n(X, A)\). |
| Application | Used to replace complicated pairs \((X,A)\) with simpler pairs \((X \setminus U, A \setminus U)\). | Measures how cycles in \(A\) differ from those in \(X\), analyzing boundaries and extensions. |
| Relation | Tool applied within relative homology to simplify pairs. | Conceptual framework for comparing spaces and subspaces homologically. |
Introduction to Excision and Relative Homology
Excision is a fundamental concept in algebraic topology that allows the removal of a subspace from a topological space without altering the relative homology groups, facilitating simpler calculations. Relative homology, defined for a pair of spaces (X, A), measures how the homology of X differs from that of A, capturing essential topological features of the pair. The excision theorem guarantees that under certain conditions, the inclusion-induced homomorphisms on relative homology are isomorphisms, which is critical for effectively computing and understanding topological invariants.
Fundamental Concepts in Algebraic Topology
Excision in algebraic topology allows for the removal of a subspace from a topological space without altering the relative homology groups, enabling easier computation and analysis. Relative homology measures the homological differences between a space and its subspace, capturing how the inclusion changes topological features. These fundamental concepts facilitate the decomposition of complex spaces into simpler parts, enhancing the study of continuous mappings and topological invariants.
Defining Excision Theorem
The Excision Theorem in algebraic topology states that removing a suitably nice subspace from a topological space does not change the relative homology groups, provided the removed subspace lies entirely within the interior of the other subspace. This theorem enables computation of relative homology by excising parts of the space, simplifying complex calculations. It is fundamental in relating the homology of pairs of spaces and enables the localization of homological properties.
Understanding Relative Homology
Relative homology measures the algebraic structure of a space X relative to a subspace A, capturing differences between their homology groups. The excision theorem enables simplification by replacing pairs (X, A) with more manageable pairs (X \ U, A \ U) without altering relative homology groups. Understanding relative homology is crucial for analyzing spaces with substructures and applying excision to compute topological invariants efficiently.
Relationship between Excision and Relative Homology
Excision theorem provides a powerful tool in algebraic topology by allowing the removal of a subspace from a pair without changing the relative homology groups, establishing an isomorphism between the relative homology of the original pair and the pair with the excised subspace removed. This relationship simplifies the computation of relative homology groups by replacing complicated spaces with simpler, homologically equivalent pairs. Excision ensures that the relative homology functor is invariant under the excision of suitably nice subspaces, reinforcing the stability of homological invariants in topological spaces.
Key Examples Illustrating Excision
Excision in algebraic topology allows the removal of a subspace pair without changing relative homology groups, exemplified by the inclusion \( (X \setminus U, A \setminus U) \hookrightarrow (X, A) \) when \( U \subset A \subset X \) and \( \overline{U} \subset \mathrm{int}(A) \). A key example is the computation of the relative homology \( H_n(D^2, S^1) \), where excision removes a small disk to simplify to \( H_n(D^2 \setminus U, S^1 \setminus U) \cong H_n(D^2, S^1) \). This demonstrates how excision allows localized modifications in pairs to aid in calculating algebraic invariants without altering homological properties.
Applications of Relative Homology
Relative homology is instrumental in analyzing spaces with subspaces, particularly in algebraic topology for studying pairs (X, A) where A is a subspace of X, allowing the comparison of their homological features. This concept aids in the calculation of homology groups in complex spaces by simplifying the analysis through quotients and exact sequences, relevant in fields like manifold theory and topological data analysis. Unlike excision, which provides conditions to replace certain subspaces without altering homology, relative homology directly facilitates the study of spaces with boundaries or singularities, making it essential in applications such as Morse theory and persistent homology.
Common Misconceptions and Limitations
Excision in algebraic topology is often mistakenly believed to apply universally, but it only holds under conditions involving good pairs of spaces, limiting its direct application in complex or pathological cases. Relative homology, while useful for studying spaces with subspaces, sometimes faces misinterpretations regarding its invariance properties and exactness in long exact sequences. Both concepts require careful consideration of the underlying chain complexes and topological pairs to avoid errors in homological computations.
Excision in Computational Topology
Excision in computational topology facilitates the calculation of homology groups by enabling the removal of subspaces without altering relative homology, streamlining complex space analysis. This principle ensures that under suitable conditions, the homology of a pair (X, A) remains invariant when a subspace B contained in A is excised, crucial for efficient algorithmic implementations. Excision aids in breaking down large simplicial complexes into manageable parts, improving computational efficiency in persistent homology and topological data analysis.
Summary and Further Reading
Excision theorem in algebraic topology allows for the replacement of a subspace with a homotopy equivalent subspace without changing the relative homology groups, facilitating simpler computations. Relative homology groups measure the homology of a space relative to a subspace, capturing the features that are present in the larger space but not in the subspace. For further reading, explore Hatcher's "Algebraic Topology" for comprehensive explanations and examples, and consult Spanier's "Algebraic Topology" for detailed discussions on excision and relative homology properties.
Excision Infographic
 libterm.com
libterm.com