Modules help you organize complex systems into manageable, reusable components that enhance maintainability and scalability. Understanding how to effectively design and implement modules can significantly improve your development workflow and project structure. Discover practical tips and insights in the rest of this article to optimize your module usage.
Table of Comparison
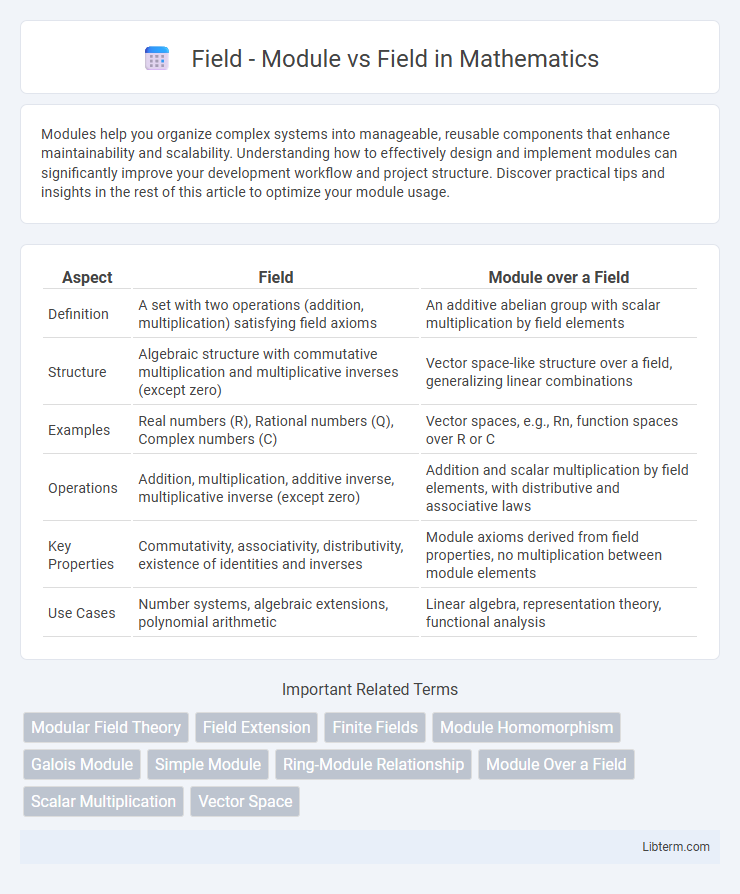
| Aspect | Field | Module over a Field |
|---|---|---|
| Definition | A set with two operations (addition, multiplication) satisfying field axioms | An additive abelian group with scalar multiplication by field elements |
| Structure | Algebraic structure with commutative multiplication and multiplicative inverses (except zero) | Vector space-like structure over a field, generalizing linear combinations |
| Examples | Real numbers (R), Rational numbers (Q), Complex numbers (C) | Vector spaces, e.g., Rn, function spaces over R or C |
| Operations | Addition, multiplication, additive inverse, multiplicative inverse (except zero) | Addition and scalar multiplication by field elements, with distributive and associative laws |
| Key Properties | Commutativity, associativity, distributivity, existence of identities and inverses | Module axioms derived from field properties, no multiplication between module elements |
| Use Cases | Number systems, algebraic extensions, polynomial arithmetic | Linear algebra, representation theory, functional analysis |
Introduction: Understanding Fields and Modules
Fields represent individual data points or attributes within a database or form, while modules are comprehensive containers that group related fields to manage complex data structures effectively. Understanding the distinction between fields and modules is crucial for database design, as fields capture specific pieces of information whereas modules organize these fields into functional units. This hierarchical structure enhances data management, scalability, and clarity in software applications and content management systems.
Defining Fields in Mathematics
Defining fields in mathematics involves establishing algebraic structures where operations of addition, subtraction, multiplication, and division (excluding division by zero) are well-defined and satisfy specific axioms. A field module, or vector space, extends this concept by considering a set equipped with both field elements and an abelian group structure, enabling scalar multiplication that adheres to compatibility rules with field operations. Understanding the distinction between pure fields and field modules is crucial for applications in linear algebra, algebraic geometry, and module theory.
Defining Modules and Their Structure
Defining modules in software development involves grouping related fields into a cohesive structure that enhances maintainability and reusability. Each module encapsulates a set of fields and functions, promoting modular design and reducing code complexity. Structuring modules correctly ensures clear boundaries and interaction patterns, optimizing both development workflow and system scalability.
Key Differences Between Fields and Modules
Fields define individual data elements within a record, such as name or date, while modules serve as containers grouping related fields and functionalities into distinct sections of a software system. Modules organize data management and user interface components, enabling efficient access and customization of business processes, whereas fields capture specific data points for storage and retrieval. The key difference lies in their scope: fields represent single data attributes, and modules encompass broader structural units integrating multiple fields and features.
Algebraic Properties of Fields
Fields are algebraic structures consisting of a set equipped with two operations, addition and multiplication, satisfying commutativity, associativity, distributivity, existence of identity elements, and invertibility of non-zero elements. A field module, or vector space over a field, extends these properties by introducing scalar multiplication, enabling linear combinations and preserving the field's algebraic properties. The interplay between fields and field modules underpins fundamental algebraic concepts such as linear independence, dimension, and basis in vector space theory.
The Role of Rings in Module Theory
Rings serve as the foundational algebraic structures governing modules, analogous to how fields underpin vector spaces, providing the operations necessary for scalar multiplication within module theory. Unlike fields, rings may lack multiplicative inverses, resulting in modules exhibiting more complex behaviors and richer structural diversity compared to vector spaces. The interaction between rings and modules forms the core of module theory, enabling the extension of linear algebra concepts to broader algebraic systems.
Examples: Fields vs. Modules in Practice
Fields represent individual data points such as text, numbers, or dates, used to capture specific information within a form or database. Modules are collections of related fields grouped to organize and manage complex data structures, like a "Customer" module containing fields for name, contact details, and purchase history. For example, a CRM system uses a "Fields" approach to store a customer's phone number, while a "Modules" structure aggregates multiple fields into a single customer record for comprehensive data management.
Applications of Fields and Modules
Fields, fundamental in algebra, support operations of addition, subtraction, multiplication, and division, crucial in applications like coding theory and cryptography, ensuring secure data transmission. Modules, generalizing vector spaces by allowing scalars from rings rather than fields, are essential in algebraic topology and homological algebra for studying complex structures and invariants. Both structures underpin computational algorithms in computer science and influence the design of error-correcting codes and signal processing techniques.
Common Misconceptions: Field or Module?
A common misconception is confusing a Field with a Module in database and software development contexts. A Field represents a single data attribute or column within a database table, while a Module refers to a collection of related Fields or components grouped to perform a specific functionality. Understanding that Fields are atomic data units and Modules are higher-level organizational structures helps clarify their distinct roles in system design.
Conclusion: Choosing Between Field and Module
Choosing between Field and Module depends largely on project scope and integration needs. Fields offer granular control for individual data points within forms, ideal for targeted data collection and customization. Modules provide a more comprehensive solution, bundling related functionalities and enabling scalable, streamlined management across larger applications.
Field - Module Infographic
 libterm.com
libterm.com