An inflection point marks a change in the curvature of a function, where its concavity shifts from upward to downward or vice versa, indicating crucial transitions in mathematical analysis and real-world data trends. Understanding inflection points helps you identify moments of acceleration or deceleration in growth patterns, essential for fields like economics, engineering, and biology. Explore the rest of this article to learn how to locate and interpret inflection points effectively.
Table of Comparison
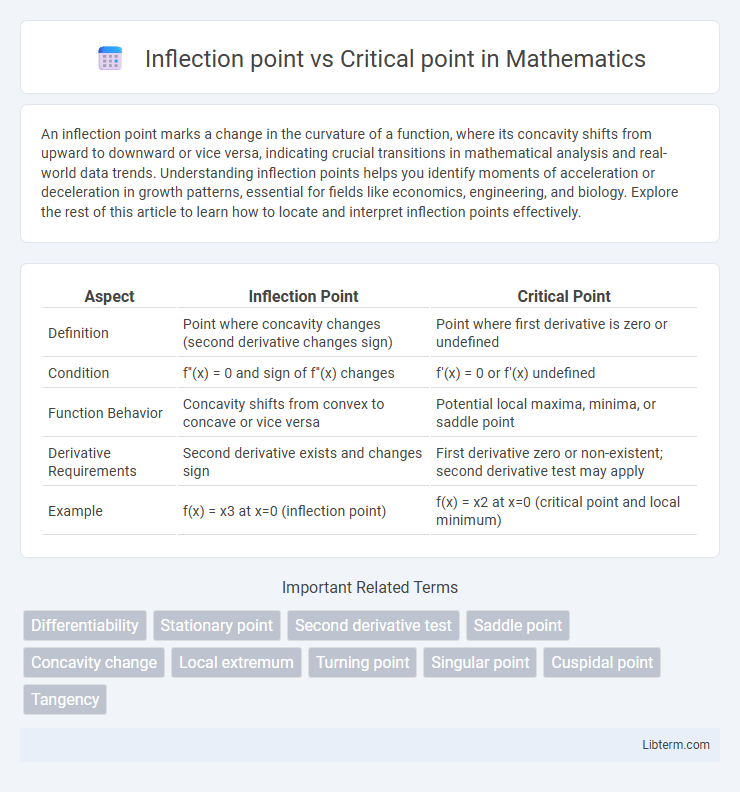
| Aspect | Inflection Point | Critical Point |
|---|---|---|
| Definition | Point where concavity changes (second derivative changes sign) | Point where first derivative is zero or undefined |
| Condition | f''(x) = 0 and sign of f''(x) changes | f'(x) = 0 or f'(x) undefined |
| Function Behavior | Concavity shifts from convex to concave or vice versa | Potential local maxima, minima, or saddle point |
| Derivative Requirements | Second derivative exists and changes sign | First derivative zero or non-existent; second derivative test may apply |
| Example | f(x) = x3 at x=0 (inflection point) | f(x) = x2 at x=0 (critical point and local minimum) |
Understanding Inflection Points
Inflection points occur where the concavity of a function changes, marked by the second derivative shifting sign from positive to negative or vice versa, indicating a transition in the curve's curvature. Unlike critical points, which involve where the first derivative is zero or undefined and often correspond to local maxima or minima, inflection points may not correspond to any extremum but signal changes in the function's acceleration behavior. Understanding inflection points is crucial for analyzing the shape and behavior of graphs in calculus, optimization, and applied mathematics.
Defining Critical Points
Critical points are specific values in a function's domain where the derivative is zero or undefined, indicating potential local maxima, minima, or saddle points. Inflection points occur where the second derivative changes sign, marking a shift in the concavity of the function. Understanding critical points is essential for analyzing a function's behavior, as they highlight where the slope flattens or the function's growth changes direction.
Key Differences Between Inflection and Critical Points
Inflection points occur where the concavity of a function changes, marked by the second derivative shifting signs, whereas critical points happen where the first derivative equals zero or is undefined, indicating potential local maxima, minima, or saddle points. Inflection points do not necessarily correspond to local extrema, while critical points are key candidates for identifying those extrema. Understanding these distinctions is essential in calculus for accurately analyzing function behavior and curve sketching.
Mathematical Interpretation of Inflection Points
An inflection point in calculus is where a function changes concavity, identified by a sign change in the second derivative \( f''(x) \), but not necessarily where \( f''(x) = 0 \) alone. A critical point occurs where the first derivative \( f'(x) \) is zero or undefined, indicating potential local maxima, minima, or saddle points. Distinguishing inflection points requires analyzing \( f''(x) \) behavior to confirm concavity shifts, whereas critical points focus on where the slope flattens.
Mathematical Interpretation of Critical Points
Critical points in calculus are defined as values of the domain where the derivative of a function is zero or undefined, indicating potential local maxima, minima, or saddle points. Inflection points occur where the concavity of the function changes, typically identified by the second derivative changing sign, but the first derivative may not necessarily be zero at these points. Understanding critical points involves examining the first and second derivatives to determine the nature of extrema and assess function behavior at those specific inputs.
Graphical Representation and Visualization
An inflection point on a graph is where the curve changes concavity, shifting from concave up to concave down or vice versa, often marked by a zero second derivative without a local maximum or minimum. A critical point occurs where the first derivative is zero or undefined, indicating potential local maxima, minima, or saddle points, and is visually identified as peaks, troughs, or flat tangents on the graph. Graphically, inflection points are notable for curvature changes without extremum values, while critical points highlight stationary points where the slope of the tangent line is horizontal or non-existent.
Applications in Calculus and Real-World Problems
Inflection points highlight where a function's concavity changes, essential for understanding curve behavior in optimization problems and economic models, while critical points identify where the derivative is zero or undefined, indicating potential maxima, minima, or saddle points. In calculus, analyzing both is crucial for sketching graphs and solving optimization tasks, such as maximizing profit or minimizing cost. Real-world applications include engineering design for stress analysis, where inflection points indicate changes in bending, and critical points guide optimal resource allocation or decision-making thresholds.
Common Misconceptions and Clarifications
Common misconceptions often confuse inflection points with critical points by assuming both represent locations where a function's behavior changes dramatically. An inflection point occurs where the concavity of a function changes sign, indicated by the second derivative shifting from positive to negative or vice versa, while a critical point occurs where the first derivative is zero or undefined, signaling potential local maxima, minima, or saddle points. Clarifying that not all critical points are inflection points, and not all inflection points coincide with critical points, helps accurately analyze the function's graph and behavior.
How to Identify Inflection and Critical Points
Inflection points occur where the second derivative of a function changes sign, indicating a change in concavity, and they can be identified by solving for points where the second derivative equals zero or is undefined, confirming a sign change on either side. Critical points are found by setting the first derivative equal to zero or identifying where it does not exist, representing potential local maxima, minima, or saddle points. Verifying the nature of these points requires analyzing the first and second derivatives using tests like the second derivative test or the first derivative test.
Summary Table: Inflection Point vs. Critical Point
The summary table highlights key differences between inflection points and critical points in calculus: inflection points occur where the second derivative changes sign, indicating a change in concavity, while critical points occur where the first derivative is zero or undefined, marking potential local maxima, minima, or saddle points. Inflection points do not necessarily correspond to extrema, whereas critical points are candidates for these features. Understanding these distinctions aids in graph analysis and function behavior characterization.
Inflection point Infographic
 libterm.com
libterm.com