Spiegelung is a fundamental concept in geometry involving the reflection of points or shapes across a line or plane, creating a mirror image that preserves size and shape but reverses orientation. This transformation plays a crucial role in various applications, from computer graphics to architectural design, where symmetry and balance are essential. Explore the rest of the article to discover how Spiegelung techniques can enhance your understanding of spatial relationships and practical uses.
Table of Comparison
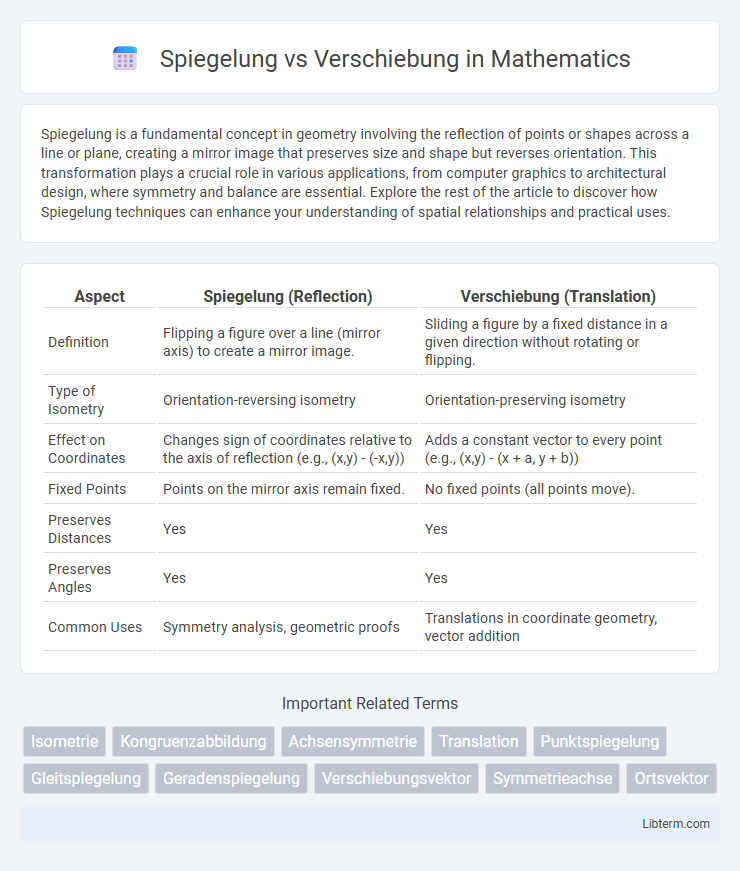
| Aspect | Spiegelung (Reflection) | Verschiebung (Translation) |
|---|---|---|
| Definition | Flipping a figure over a line (mirror axis) to create a mirror image. | Sliding a figure by a fixed distance in a given direction without rotating or flipping. |
| Type of Isometry | Orientation-reversing isometry | Orientation-preserving isometry |
| Effect on Coordinates | Changes sign of coordinates relative to the axis of reflection (e.g., (x,y) - (-x,y)) | Adds a constant vector to every point (e.g., (x,y) - (x + a, y + b)) |
| Fixed Points | Points on the mirror axis remain fixed. | No fixed points (all points move). |
| Preserves Distances | Yes | Yes |
| Preserves Angles | Yes | Yes |
| Common Uses | Symmetry analysis, geometric proofs | Translations in coordinate geometry, vector addition |
Einführung in Spiegelung und Verschiebung
Spiegelung and Verschiebung are fundamental concepts in geometry representing reflection and translation, respectively. Spiegelung involves flipping a figure over a specific axis or line, creating a mirror image that preserves shape and size but reverses orientation. Verschiebung shifts every point of a figure by the same distance in a particular direction, maintaining both orientation and congruence without altering the figure's shape.
Definition von Spiegelung
Spiegelung bezeichnet in der Geometrie die Abbildung, bei der jeder Punkt eines Objekts an einer Spiegelachse oder -ebene so reflektiert wird, dass der Abstand zum Spiegelbildpunkt gleich bleibt und die Verbindungslinie zwischen den Punkten senkrecht zur Spiegelachse steht. Verschiebung hingegen beschreibt eine Parallelverschiebung eines Objekts um einen bestimmten Vektor, wobei die Orientierung und Form unverandert bleiben. Spiegelung andert die Orientierung des Objekts, wahrend Verschiebung sie bewahrt.
Definition von Verschiebung
Verschiebung, in der Geometrie, bezeichnet die Translation eines Objekts entlang eines Vektors, wodurch alle Punkte des Objekts um denselben Abstand und in dieselbe Richtung verschoben werden. Im Gegensatz zur Spiegelung verandert die Verschiebung die Orientierung des Objekts nicht, sondern erhalt sie bei. Die Verschiebung wird durch den Verschiebungsvektor definiert, der Exakte Richtungs- und Langeninformationen der Bewegung liefert.
Mathematische Grundlagen beider Transformationen
Spiegelung und Verschiebung sind fundamentale Transformationen in der Geometrie mit klar definierten mathematischen Grundlagen. Eine Spiegelung lasst sich als Isometrie darstellen, bei der jeder Punkt P bezuglich einer Geraden (Spiegelebene im Raum) auf einen Punkt P' abgebildet wird, sodass die Gerade die Mittelsenkrechte der Strecke PP' ist. Die Verschiebung, auch Translation genannt, ist eine Bewegung, bei der alle Punkte eines Korpers oder Koordinatensystems um denselben Vektor \(\vec{v}\) verschoben werden, formal ausgedruckt als \(P' = P + \vec{v}\), wobei Lange und Orientierung der Figur unverandert bleiben.
Spiegelung: Eigenschaften und Anwendungen
Spiegelung, eine fundamentale geometrische Transformation, erzeugt ein spiegelbildliches Abbild eines Objekts an einer bestimmten Achse oder Ebene, wobei die Abstande zu dieser Spiegelachse erhalten bleiben. Zu den Eigenschaften zahlen die Orientierungumkehr und die Isometrie, welche die Form und Grosse des Objekts unverandert lassen. Anwendungen der Spiegelung finden sich in der Grafik, Architektur, optischen Systemen und der Computergrafik, insbesondere bei der symmetrischen Modellierung und Bildbearbeitung.
Verschiebung: Eigenschaften und Anwendungen
Verschiebung, eine grundlegende Transformation in der Geometrie, bewirkt die Verschiebung aller Punkte einer Figur um einen festen Vektor ohne Anderung ihrer Form oder Grosse. Eigenschaften wie Parallelitat und Abstand zwischen Punkten bleiben bei der Verschiebung erhalten, wodurch sie isometrisch ist. Anwendungen der Verschiebung finden sich in der Computergrafik zur Positionierung von Objekten, in der Robotik zur Pfadplanung und in der Physik zur Beschreibung von Bewegungen ohne Drehungen.
Unterschied zwischen Spiegelung und Verschiebung
Der Hauptunterschied zwischen Spiegelung und Verschiebung liegt in der Art der geometrischen Transformation: Spiegelung erzeugt ein Bild, das an einer Achse oder Ebene reflektiert wird, wodurch eine Umkehrung der Orientierung stattfindet, wahrend Verschiebung die Figur parallel in eine andere Position bewegt, ohne die Form oder Orientierung zu verandern. Spiegelung verandert die relativen Positionen der Punkte zueinander durch Reflexion, Verschiebung verschiebt alle Punkte um denselben Vektor, wodurch die Figur lediglich verschoben wird. Beide Transformationen sind isometrisch, erhalten also Winkel, Langen und Formen, unterscheiden sich jedoch in der Veranderung der Lage und Orientierung der Figur.
Praxisbeispiele und Visualisierung
Spiegelung und Verschiebung sind grundlegende Transformationen in der Geometrie, die sich durch ihre Anwendung und Visualisierung unterscheiden. Bei der Spiegelung werden Punkte an einer Spiegelachse reflektiert, was in Praxisbeispielen wie der Erstellung symmetrischer Muster oder der Bildbearbeitung besonders sichtbar wird. Verschiebung beschreibt die gleichmassige Verschiebung aller Punkte um einen festen Vektor, haufig genutzt in der Robotik und Grafikprogrammierung fur Bewegungsdarstellungen und Animationen.
Häufige Fehler und Missverständnisse
Spiegelung und Verschiebung werden oft verwechselt, weil beide geometrische Transformationen sind, die Punkte im Raum verschieben, jedoch unterschiedliche Eigenschaften besitzen. Haufige Fehler entstehen, wenn Spiegelungen falschlicherweise als Verschiebungen interpretiert werden, was zu falschen Positionen und Orientierungen der Objekte fuhrt. Missverstandnisse treten auch auf, wenn die Achse oder Ebene der Spiegelung nicht korrekt bestimmt wird, was die Symmetrieeigenschaften erheblich beeinflusst.
Zusammenfassung und Fazit
Spiegelung involviert die Reflexion eines Objekts an einer Achse oder Ebene, wodurch eine spiegelbildliche Umkehrung entsteht, wahrend Verschiebung eine parallel verlaufende Translation ohne Richtungsanderung darstellt. Beide Transformationen sind Teil der euklidischen Geometrie und erhalten Abstande sowie Winkel zwischen Punkten, unterscheiden sich jedoch in der Veranderung der Orientierung. Insgesamt ermoglicht die Spiegelung eine symmetrische Abbildung, wahrend die Verschiebung die Position erhalt, was fur geometrische Konstruktionen und Analysen grundlegend ist.
Spiegelung Infographic
 libterm.com
libterm.com