NP-complete problems represent a class of computational challenges that are both in NP and as hard as any problem in NP, meaning they can be verified quickly but no efficient solution method is known. Understanding NP-completeness is crucial for fields that require solving complex problems, such as cryptography, optimization, and algorithm design. Explore the rest of the article to grasp how NP-completeness impacts your approach to problem-solving in computer science.
Table of Comparison
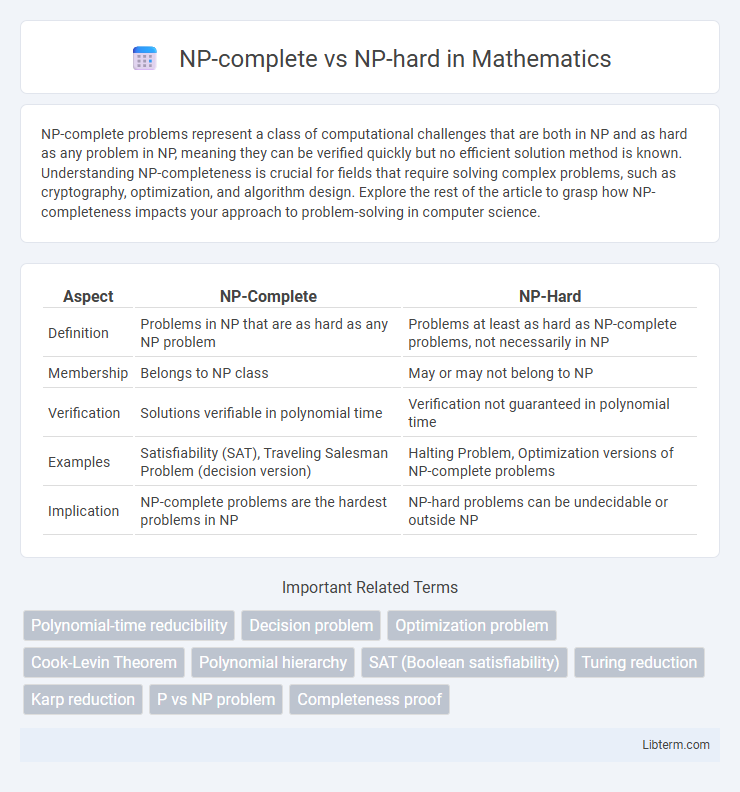
| Aspect | NP-Complete | NP-Hard |
|---|---|---|
| Definition | Problems in NP that are as hard as any NP problem | Problems at least as hard as NP-complete problems, not necessarily in NP |
| Membership | Belongs to NP class | May or may not belong to NP |
| Verification | Solutions verifiable in polynomial time | Verification not guaranteed in polynomial time |
| Examples | Satisfiability (SAT), Traveling Salesman Problem (decision version) | Halting Problem, Optimization versions of NP-complete problems |
| Implication | NP-complete problems are the hardest problems in NP | NP-hard problems can be undecidable or outside NP |
Introduction to Computational Complexity
NP-complete problems are a subset of NP problems characterized by their ability to be verified in polynomial time and their equivalence in complexity to every problem in NP, making them both verifiable and as hard as the hardest problems in NP. NP-hard problems, by contrast, are at least as hard as NP-complete problems but are not necessarily in NP themselves, often lacking polynomial-time verification. Understanding these distinctions is fundamental in computational complexity because it helps classify decision problems based on their inherent difficulty and the feasibility of algorithmic solutions.
Defining NP-complete Problems
NP-complete problems are decision problems within NP (nondeterministic polynomial time) class that are both verifiable in polynomial time and as hard as any problem in NP, meaning every NP problem can be polynomially reduced to them. These problems serve as benchmarks for computational complexity, indicating that if any NP-complete problem is solved in polynomial time, all problems in NP can be efficiently solved. Defining NP-complete problems requires proving that a problem belongs to NP and demonstrating a polynomial-time reduction from an already known NP-complete problem.
Understanding NP-hard Problems
NP-hard problems represent a class of computational challenges that are at least as difficult as the hardest problems in NP, meaning there is no known polynomial-time algorithm to solve them. Unlike NP-complete problems, NP-hard problems do not have to be in NP, so they may not be decision problems or verifiable in polynomial time. Understanding NP-hard problems is crucial for algorithm design and complexity theory, as they define the boundaries of computational feasibility and guide researchers in identifying problems that require approximation or heuristic methods.
Key Differences Between NP-complete and NP-hard
NP-complete problems are a subset of NP-hard problems characterized by being both in NP and as difficult as any problem in NP, meaning they have solutions verifiable in polynomial time. NP-hard problems encompass all problems at least as hard as NP-complete ones but are not necessarily in NP, implying their solutions may not be verifiable in polynomial time. The critical distinction lies in NP-complete problems requiring membership in NP, while NP-hard problems encompass a broader range, including those outside NP, often without known polynomial verification methods.
Examples of NP-complete Problems
Classic examples of NP-complete problems include the Traveling Salesman Problem, the Boolean Satisfiability Problem (SAT), and the Knapsack Problem. These problems are both in NP and as hard as any problem in NP, meaning a polynomial-time solution to one NP-complete problem would solve all NP problems efficiently. NP-hard problems, by contrast, may not be in NP but are at least as difficult as NP-complete problems, often including optimization or decision problems beyond NP.
Examples of NP-hard Problems
NP-hard problems include classic examples such as the Traveling Salesman Problem, the Knapsack Problem, and the Boolean Satisfiability Problem (SAT). These problems are at least as hard as the hardest problems in NP, but they do not necessarily belong to NP themselves, often lacking efficient solutions or verifiable certificates. Understanding NP-hard problems is crucial for fields like operations research, cryptography, and algorithm design due to their computational complexity and intractability in large instances.
Importance in Computer Science and Real-world Applications
NP-complete problems are pivotal in computer science as they represent the hardest problems within NP, offering a benchmark for evaluating algorithmic efficiency and complexity theory, and their solutions impact fields like cryptography, optimization, and artificial intelligence. NP-hard problems extend this complexity by encompassing even more challenging tasks that may not be verifiable in polynomial time, highlighting critical boundaries in problem-solving capabilities. Practical applications include scheduling optimization, network design, and decision-making systems, where understanding the nuances between NP-complete and NP-hard guides the development of heuristics and approximation algorithms essential for tackling large-scale, real-world computational challenges.
Techniques for Identifying NP-complete and NP-hard Problems
Techniques for identifying NP-complete problems often involve polynomial-time reductions from known NP-complete problems, utilizing Cook-Levin theorem and Karp reductions to demonstrate equivalence in computational complexity. NP-hard problems are typically recognized by showing a polynomial-time reduction from an NP-complete problem to the problem in question, indicating at least equal computational difficulty without requiring membership in NP. Complexity theory frameworks such as the use of decision versions, problem transformations, and verification via nondeterministic polynomial-time algorithms are critical in classifying problems as NP-complete or NP-hard.
Approaches to Solving or Approximating These Problems
Approaches to solving NP-complete problems typically involve heuristic algorithms, approximation algorithms, and exponential-time exact algorithms, whereas NP-hard problems often require relaxation techniques, problem reductions, or use of probabilistic and metaheuristic methods like genetic algorithms and simulated annealing. Approximation algorithms provide near-optimal solutions with provable bounds primarily for NP-complete problems, while for NP-hard problems without known polynomial-time approximations, researchers rely on parameterized complexity and fixed-parameter tractable (FPT) algorithms. Integer linear programming (ILP) formulations and branch-and-bound methods are extensively used for both problem classes to find exact or approximate solutions in practical computational time.
Future Challenges and Research Directions
NP-complete problems represent the subset of NP-hard problems that are both verifiable and as difficult as the hardest problems in NP, posing significant challenges for algorithm design and optimization. Future research directions involve developing more efficient approximation algorithms, exploring quantum computing techniques, and creating hybrid classical-quantum models to better address these computational barriers. Advances in complexity theory and heuristic methods are critical to overcoming the limitations in solving NP-complete and NP-hard problems within practical time frames.
NP-complete Infographic
 libterm.com
libterm.com