Projective techniques unlock deeper insights by revealing subconscious thoughts and feelings that traditional methods often miss. They help you interpret ambiguous stimuli, offering a richer understanding of motivations and behaviors. Explore the rest of the article to discover how projective methods can transform your approach to research and analysis.
Table of Comparison
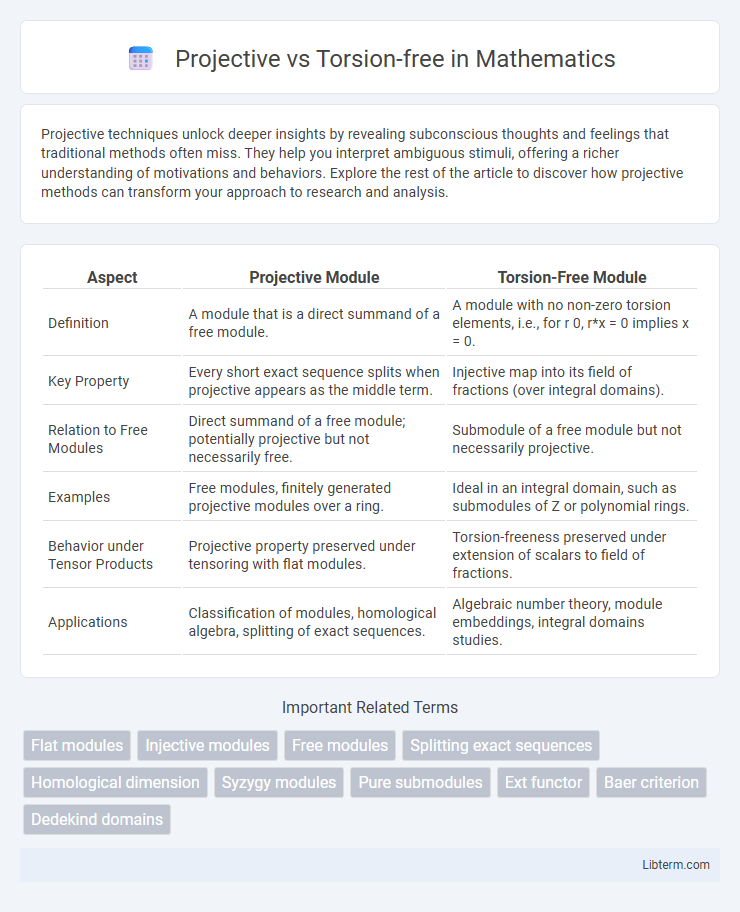
| Aspect | Projective Module | Torsion-Free Module |
|---|---|---|
| Definition | A module that is a direct summand of a free module. | A module with no non-zero torsion elements, i.e., for r 0, r*x = 0 implies x = 0. |
| Key Property | Every short exact sequence splits when projective appears as the middle term. | Injective map into its field of fractions (over integral domains). |
| Relation to Free Modules | Direct summand of a free module; potentially projective but not necessarily free. | Submodule of a free module but not necessarily projective. |
| Examples | Free modules, finitely generated projective modules over a ring. | Ideal in an integral domain, such as submodules of Z or polynomial rings. |
| Behavior under Tensor Products | Projective property preserved under tensoring with flat modules. | Torsion-freeness preserved under extension of scalars to field of fractions. |
| Applications | Classification of modules, homological algebra, splitting of exact sequences. | Algebraic number theory, module embeddings, integral domains studies. |
Introduction to Projective and Torsion-free Modules
Projective modules are direct summands of free modules, characterized by their lifting property which ensures exactness in homological algebra, making them fundamental in module theory. Torsion-free modules over an integral domain lack elements annihilated by nonzero domain elements, preserving injectivity of scalar multiplication and often serving as generalizations of free modules. Understanding projective and torsion-free modules is essential for exploring module decompositions and homological dimensions in algebraic structures.
Defining Projective Modules
Projective modules are defined as direct summands of free modules, characterized by the lifting property that any module homomorphism from a projective module to a quotient module can be lifted to a homomorphism to the original module. Unlike torsion-free modules, projective modules guarantee the splitting of exact sequences, making them foundational in homological algebra and module theory. This structural flexibility distinguishes projective modules by ensuring they remain free from extension obstructions, unlike general torsion-free modules which only avoid elements annihilated by nonzero scalars.
Defining Torsion-free Modules
Torsion-free modules are defined as modules over an integral domain where no nonzero element is annihilated by a nonzero scalar, ensuring the absence of elements with "torsion." In contrast, projective modules are direct summands of free modules characterized by the lifting property that facilitates module homomorphisms, but they may contain torsion elements depending on the ring. The distinction hinges on torsion-free modules maintaining injectivity under scalar multiplication by nonzero ring elements, whereas projective modules emphasize structural decomposability and homological properties.
Key Differences Between Projective and Torsion-free
Projective modules are direct summands of free modules and possess a lifting property that facilitates module homomorphisms, whereas torsion-free modules are characterized by having no elements annihilated by nonzero scalars in integral domains. Projective modules ensure exactness in sequences due to their splitting properties, while torsion-free modules primarily guarantee the absence of torsion elements, impacting divisibility and injectivity but not necessarily projectivity. The key distinction lies in their structural roles: projective modules relate to module decomposition and homological algebra, whereas torsion-free modules focus on element-wise divisibility within their ring.
Algebraic Structures Involving Projective Modules
Projective modules play a critical role in algebraic structures due to their property of lifting homomorphisms, which ensures exact sequence splitting and facilitates module decomposition. Torsion-free modules, important in integral domains, lack elements annihilated by nonzero scalars, making them essential in the study of free and projective modules over integral domains. Understanding the interplay between projective and torsion-free modules allows deeper insights into ring theory and homological algebra, especially in characterizing module types and their extensions.
Examples of Torsion-free Modules
Torsion-free modules over an integral domain, such as the ring of integers \(\mathbb{Z}\), are exemplified by free modules like \(\mathbb{Z}^n\), which contain no elements annihilated by nonzero ring elements. Projective modules, while always torsion-free in domains, include direct summands of free modules, for example, \(\mathbb{Z}\)-submodules of \(\mathbb{Q}^n\) that split off as summands. Examples of torsion-free modules also arise in algebraic geometry, such as torsion-free sheaves over integral schemes, which encapsulate modules without torsion elements but may not be projective.
Homological Properties Compared
Projective modules exhibit homological properties characterized by their ability to lift module homomorphisms and their existence as direct summands of free modules, resulting in vanishing higher Ext groups and finite projective dimension. Torsion-free modules lack elements annihilated by nonzero scalars, enhancing their role in domains without zero divisors but do not guarantee finite projective dimension or splitting properties. Compared homologically, projective modules demonstrate stronger conditions for exactness and resolutions, while torsion-free modules present subtler structural features influencing their homological behavior in diverse ring categories.
Criteria for Projectivity vs Torsion-freeness
Projective modules are characterized by the lifting property: a module \( P \) is projective if every surjective module homomorphism \( f: M \to N \) and every module homomorphism \( g: P \to N \) can be lifted to a module homomorphism \( h: P \to M \) such that \( f \circ h = g \). Torsion-free modules over an integral domain are defined by the absence of nonzero elements annihilated by nonzero elements of the ring, ensuring injectivity of the scalar multiplication map. While projectivity depends on module homomorphism lifting and direct summand decomposition of free modules, torsion-freeness hinges on the ring structure and the injectivity of multiplication by nonzero divisors.
Applications in Module Theory
Projective modules enable the decomposition of complex modules into direct summands, facilitating the classification and construction of modules with desirable lifting properties. Torsion-free modules, characterized by the absence of elements annihilated by nonzero scalars, are pivotal in extending results from free modules to more general settings, especially over integral domains. Applications in module theory leverage projective modules for splitting exact sequences, while torsion-free modules provide a framework for embedding modules into vector spaces or injective modules, crucial in representation theory and homological algebra.
Summary and Further Reading
Projective modules are direct summands of free modules characterized by lifting properties that aid in module decomposition, while torsion-free modules are modules without elements annihilated by non-zero divisors, often studied in integral domains. Understanding the distinction between projective and torsion-free modules illuminates module theory's structure, especially in homological algebra and commutative algebra contexts. For deeper insights, consult "Algebra" by Serge Lang, "Introduction to Commutative Algebra" by Atiyah and Macdonald, and survey articles in the Journal of Algebra focusing on module classification and homological properties.
Projective Infographic
 libterm.com
libterm.com