The numerical radius of an operator on a Hilbert space provides crucial insight into its behavior by measuring the maximum absolute value of its numerical range. This concept plays a significant role in understanding operator norms and spectral properties, influencing applications in functional analysis and quantum mechanics. Explore the rest of the article to deepen your understanding of the numerical radius and its mathematical significance.
Table of Comparison
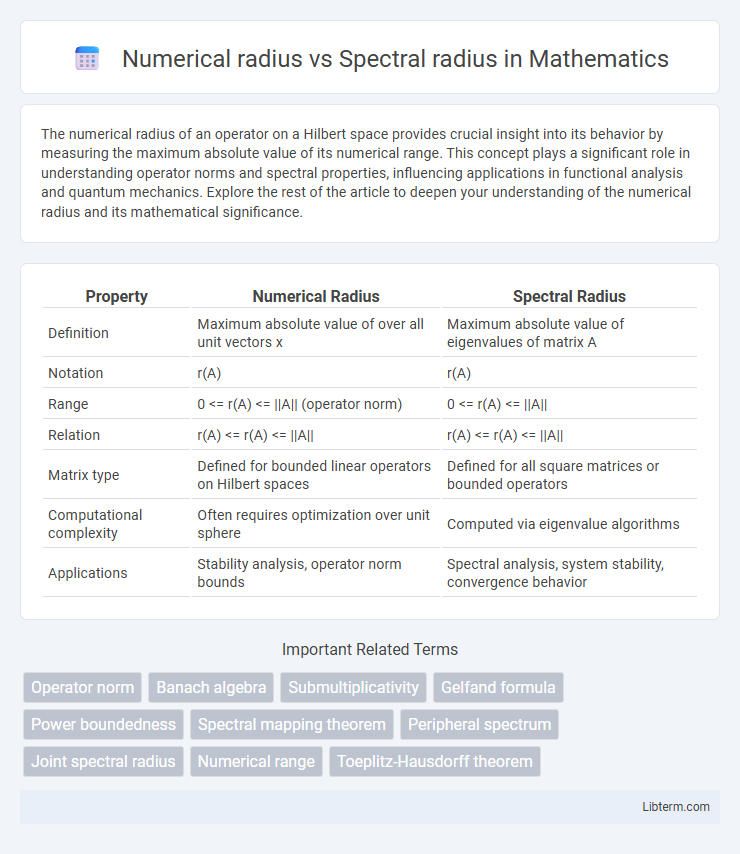
| Property | Numerical Radius | Spectral Radius |
|---|---|---|
| Definition | Maximum absolute value of |
Maximum absolute value of eigenvalues of matrix A |
| Notation | r(A) | r(A) |
| Range | 0 <= r(A) <= ||A|| (operator norm) | 0 <= r(A) <= ||A|| |
| Relation | r(A) <= r(A) <= ||A|| | r(A) <= r(A) <= ||A|| |
| Matrix type | Defined for bounded linear operators on Hilbert spaces | Defined for all square matrices or bounded operators |
| Computational complexity | Often requires optimization over unit sphere | Computed via eigenvalue algorithms |
| Applications | Stability analysis, operator norm bounds | Spectral analysis, system stability, convergence behavior |
Introduction to Numerical Radius and Spectral Radius
Numerical radius quantifies the maximum absolute value of a matrix's numerical range, serving as a crucial measure in operator theory and matrix analysis. Spectral radius represents the largest absolute eigenvalue of a matrix, often determining stability and convergence properties in linear algebra applications. Both numerical radius and spectral radius provide essential insights into matrix behavior, with numerical radius offering a tighter bound than spectral radius in many cases.
Defining the Numerical Radius
The numerical radius of a matrix is defined as the maximum absolute value of the inner product
Understanding the Spectral Radius
The spectral radius of a matrix is the largest absolute value among its eigenvalues, providing critical insights into the matrix's stability and long-term behavior. It plays a fundamental role in determining the convergence of iterative methods and stability of dynamical systems. Unlike the numerical radius, which considers the maximum of the numerical range, the spectral radius directly characterizes the dominant growth rate of matrix powers.
Key Differences Between Numerical and Spectral Radius
The numerical radius of a matrix measures the maximum absolute value of the inner product of the matrix with unit vectors, reflecting the matrix's behavior on the unit sphere, while the spectral radius denotes the largest absolute eigenvalue, capturing the matrix's asymptotic growth rate. Numerical radius is always bounded above by the operator norm and below by half the norm, often providing a tighter bound for non-normal matrices, whereas spectral radius is crucial in stability analysis and convergence studies. Unlike spectral radius, numerical radius is a norm on the space of bounded linear operators, highlighting its importance in operator theory and functional analysis.
Mathematical Properties and Inequalities
The numerical radius \( w(A) \) of a matrix \( A \) satisfies the inequality \( \frac{1}{2} \|A\| \leq w(A) \leq \|A\| \), where \( \|A\| \) is the operator norm, highlighting its norm-like behavior. It is always greater than or equal to the spectral radius \( \rho(A) \), i.e., \( \rho(A) \leq w(A) \), reflecting the fact that the spectral radius represents the maximum modulus of eigenvalues of \( A \). The numerical radius is a sub-multiplicative seminorm and satisfies the spectral radius formula, but unlike the spectral radius, it captures additional geometric information from the field of values.
Geometric Interpretation in the Complex Plane
The numerical radius of a matrix corresponds to the maximum distance from the origin to any point in its numerical range, a convex set in the complex plane representing all possible Rayleigh quotients. The spectral radius is the largest absolute value of the matrix's eigenvalues, marking the farthest eigenvalue from the origin in the complex plane. Geometrically, the numerical radius often exceeds or equals the spectral radius since the numerical range contains all eigenvalues but covers a broader region, capturing more comprehensive operator behavior beyond eigenvalues alone.
Applications in Operator Theory
Numerical radius and spectral radius are critical in operator theory for analyzing bounded linear operators on Hilbert spaces, where the numerical radius offers a tighter bound on operator norm compared to the spectral radius. The numerical radius provides essential insights into operator behavior, stability, and convergence in iterative methods used in quantum mechanics and signal processing. Spectral radius plays a key role in spectral theory, determining the asymptotic behavior of operator powers, essential for understanding invariant subspaces and spectral decompositions.
Numerical Radius vs Spectral Radius in Matrix Analysis
Numerical radius and spectral radius are key matrix analysis concepts used to assess matrix behavior, where the spectral radius is the largest absolute value of eigenvalues of a matrix, serving as a critical stability indicator. The numerical radius, defined as the maximum absolute value of the Rayleigh quotient over all unit vectors, provides a norm-like measure closely related to the operator norm and offers bounds tighter than those given by the spectral radius alone. While the spectral radius governs asymptotic properties like power convergence, the numerical radius better captures matrix norm behavior, with the inequalities \( \frac{1}{2} \|A\| \leq w(A) \leq \|A\| \) and \( \rho(A) \leq w(A) \leq \|A\| \) emphasizing their comparative roles in matrix norms and stability analysis.
Practical Implications in Stability and Control
Numerical radius and spectral radius are critical metrics in assessing matrix behavior, with the spectral radius representing the largest absolute eigenvalue and the numerical radius indicating the maximum of the Rayleigh quotient. In stability and control applications, the numerical radius often provides a tighter bound for operator norms, offering enhanced insights into system robustness against perturbations. Engineers leverage the numerical radius to design controllers that ensure stability margins exceed spectral radius constraints, improving system reliability under real-world conditions.
Concluding Remarks and Further Research Directions
The numerical radius often provides a tighter bound on operator norms compared to the spectral radius, revealing nuanced insights into matrix behavior in functional analysis. Future research could explore the interplay between numerical radius and spectral radius in non-normal operators, potentially improving stability criteria in control theory. Investigating computational methods for accurately estimating these radii in large-scale matrices remains a critical direction for advancing numerical linear algebra applications.
Numerical radius Infographic
 libterm.com
libterm.com