Borel sets form a foundational concept in measure theory, representing the smallest s-algebra containing all open sets in a given topological space. Understanding these sets is crucial for analyzing measurable functions, probability measures, and integrating complex functions. Explore the article to deepen your grasp of Borel sets and their significant applications in mathematics.
Table of Comparison
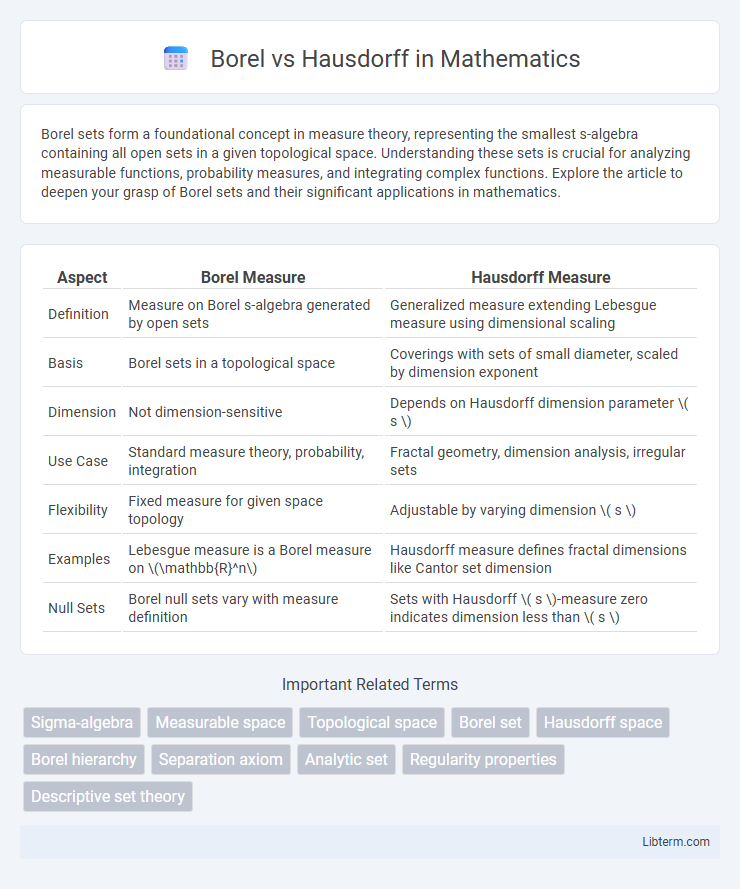
| Aspect | Borel Measure | Hausdorff Measure |
|---|---|---|
| Definition | Measure on Borel s-algebra generated by open sets | Generalized measure extending Lebesgue measure using dimensional scaling |
| Basis | Borel sets in a topological space | Coverings with sets of small diameter, scaled by dimension exponent |
| Dimension | Not dimension-sensitive | Depends on Hausdorff dimension parameter \( s \) |
| Use Case | Standard measure theory, probability, integration | Fractal geometry, dimension analysis, irregular sets |
| Flexibility | Fixed measure for given space topology | Adjustable by varying dimension \( s \) |
| Examples | Lebesgue measure is a Borel measure on \(\mathbb{R}^n\) | Hausdorff measure defines fractal dimensions like Cantor set dimension |
| Null Sets | Borel null sets vary with measure definition | Sets with Hausdorff \( s \)-measure zero indicates dimension less than \( s \) |
Introduction to Borel and Hausdorff Concepts
Borel sets refer to the s-algebra generated by open sets in a topological space, playing a fundamental role in measure theory and probability. Hausdorff spaces, defined by the separation axiom T2, ensure that any two distinct points have disjoint neighborhoods, providing a key condition for uniqueness of limits and convergence. Both concepts serve as foundational elements in topology and analysis, influencing the structure and classification of spaces.
Historical Background of Borel and Hausdorff
Emile Borel laid the foundation of measure theory in the late 19th century by introducing Borel sets, which are generated from open intervals through countable unions and intersections. Felix Hausdorff expanded on Borel's work around 1914 by formalizing topological spaces and developing the Hausdorff dimension, a key concept in fractal geometry. Their combined contributions established critical frameworks for modern topology and measure theory.
Fundamental Definitions: Borel vs Hausdorff
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the smallest s-algebra containing all open subsets in a topological space. Hausdorff spaces, defined by the T2 separation axiom, require that any two distinct points have disjoint neighborhoods, ensuring unique limits for sequences and nets. The fundamental distinction lies in Borel sets focusing on measurable structures derived from topology, while Hausdorff spaces emphasize separation properties critical for topological uniqueness and continuity.
Properties of Borel Sets
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the smallest s-algebra containing all open sets in a given topological space. They exhibit important closure properties, being closed under countable set operations, which makes them foundational in measure theory and probability. In contrast, Hausdorff spaces focus on separation axioms, ensuring distinct points have disjoint neighborhoods, a topological property not directly related to the algebraic structure of Borel sets.
Properties of Hausdorff Measures
Hausdorff measures generalize Lebesgue measure by assigning sizes to sets in metric spaces using dimension-dependent scaling, enabling the measurement of fractal and irregular sets where Borel measures may fail. Unlike Borel measures, Hausdorff measures are defined through coverings with arbitrarily small diameters, providing fine control over the measure's dimension parameter, which characterizes sets with non-integer dimensions. Key properties include s-additivity, monotonicity, and the ability to distinguish between sets of different fractal dimensions, making them essential for geometric measure theory and fractal analysis.
Key Differences Between Borel and Hausdorff
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the Borel sigma-algebra central to measure theory. Hausdorff spaces, defined by a separation axiom ensuring any two distinct points have disjoint neighborhoods, serve as a foundational concept in topology for distinguishing points. The key difference lies in Borel sets being a collection of measurable subsets within a topological space, while Hausdorff spaces describe a property of the topological space itself regarding point separation.
Applications in Measure Theory
Borel sets form the foundation for defining measurable sets in standard measure spaces such as the real line, while Hausdorff measures extend this framework to analyze fractal dimensions and irregular geometric structures by assigning measures based on size scales. Borel measures are crucial in probability theory and Lebesgue integration, whereas Hausdorff measures provide tools for quantifying the complexity of sets with non-integer dimensions in geometric measure theory. The interplay between Borel and Hausdorff concepts enables advanced applications in mathematical analysis, such as characterizing singular measures and studying fine properties of functions.
Relevance in Topology and Analysis
The Borel and Hausdorff concepts play crucial roles in topology and analysis, where Borel sets form the smallest s-algebra containing all open sets, enabling the formalization of measurable spaces essential for probability and integration theory. Hausdorff spaces, characterized by the separation axiom that any two distinct points have disjoint neighborhoods, ensure uniqueness of limits, which is fundamental for continuity and convergence analysis. Understanding the interplay between Borel sets in Hausdorff topologies enhances the study of measure theory, functional analysis, and descriptive set theory.
Practical Examples and Case Studies
Borel sets, fundamental in measure theory, are widely applied in probability spaces for defining measurable events, such as in stochastic processes and random variable analysis. Hausdorff measures excel in fractal geometry, enabling precise measurement of irregular sets like the Cantor set or coastline lengths, which traditional Lebesgue measures cannot handle. Practical case studies include modeling diffusion processes with Borel sigma-algebras and quantifying fractal dimensions in natural phenomena using Hausdorff dimension techniques.
Conclusion: Borel or Hausdorff?
Choosing between Borel and Hausdorff measures depends on the context of geometric measure theory problems; Borel measures are standard for defining measurable sets in topological spaces, while Hausdorff measures provide a nuanced approach to fractal dimensions and irregular sets. Hausdorff measure excels in capturing the size and structure of fractals and sets with complex geometric properties beyond the reach of Borel measures. Therefore, Hausdorff measure is preferred for detailed dimensional analysis, whereas Borel measure suits classical measure and integration frameworks.
Borel Infographic
 libterm.com
libterm.com