A Hamel basis is a set of vectors in a vector space that allows every element of the space to be expressed uniquely as a finite linear combination of these basis vectors. It plays a crucial role in understanding the structure of infinite-dimensional vector spaces and is essential in fields like functional analysis and linear algebra. Explore the rest of this article to deepen your understanding of how Hamel bases function and why they matter in advanced mathematical contexts.
Table of Comparison
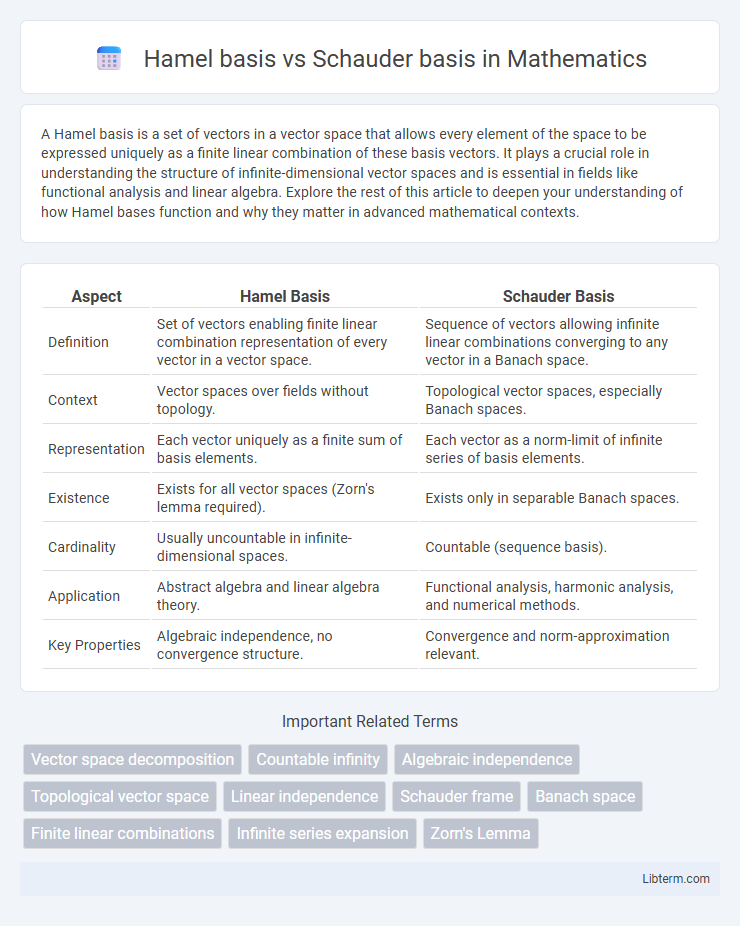
| Aspect | Hamel Basis | Schauder Basis |
|---|---|---|
| Definition | Set of vectors enabling finite linear combination representation of every vector in a vector space. | Sequence of vectors allowing infinite linear combinations converging to any vector in a Banach space. |
| Context | Vector spaces over fields without topology. | Topological vector spaces, especially Banach spaces. |
| Representation | Each vector uniquely as a finite sum of basis elements. | Each vector as a norm-limit of infinite series of basis elements. |
| Existence | Exists for all vector spaces (Zorn's lemma required). | Exists only in separable Banach spaces. |
| Cardinality | Usually uncountable in infinite-dimensional spaces. | Countable (sequence basis). |
| Application | Abstract algebra and linear algebra theory. | Functional analysis, harmonic analysis, and numerical methods. |
| Key Properties | Algebraic independence, no convergence structure. | Convergence and norm-approximation relevant. |
Introduction to Vector Space Bases
A Hamel basis in a vector space is a set of vectors such that every element of the space can be uniquely expressed as a finite linear combination of these basis vectors, emphasizing algebraic structure and finite dimensionality. In contrast, a Schauder basis allows representation of vectors as infinite convergent series of basis vectors, crucial in infinite-dimensional normed spaces like Banach spaces. This distinction highlights the difference between purely algebraic bases and topological bases in functional analysis.
Defining Hamel Basis
A Hamel basis is defined as a maximal linearly independent subset of a vector space such that every vector in the space can be expressed uniquely as a finite linear combination of basis elements. In contrast to the Schauder basis, which allows infinite series expansions converging in norm, the Hamel basis requires strictly finite representations. The existence of a Hamel basis relies on the axiom of choice and is fundamental in algebraic vector space theory rather than topological vector spaces.
Defining Schauder Basis
A Schauder basis in a Banach space is a sequence whose linear combinations converge to every element in the space with respect to the norm topology, ensuring unique representation through infinite series. Unlike a Hamel basis, which is a purely algebraic concept with finite linear combinations in vector spaces, a Schauder basis incorporates topological structure and infinite linear combinations. This distinction allows Schauder bases to apply specifically to infinite-dimensional normed spaces, providing a functional analytic framework for decomposition and approximation.
Key Differences Between Hamel and Schauder Bases
A Hamel basis is a set of vectors in a vector space such that every element can be uniquely expressed as a finite linear combination of these vectors, emphasizing algebraic span without regard to topology. A Schauder basis, defined within Banach or normed spaces, requires every element to be represented as a convergent infinite series of basis vectors, highlighting topological and analytical structure. The key difference lies in finiteness versus infinite expansions and the role of convergence, making Hamel bases suitable for pure algebraic settings and Schauder bases essential for functional analysis.
Algebraic vs. Topological Considerations
A Hamel basis consists of vectors spanning a vector space such that every element can be uniquely represented as a finite linear combination, emphasizing purely algebraic structure without regard to topology. In contrast, a Schauder basis allows infinite linear combinations that converge in a given norm, integrating topological considerations essential for functional analysis in Banach or Hilbert spaces. The distinction highlights that Hamel bases exist in all vector spaces by Zorn's lemma but are often non-constructive and impractical for infinite-dimensional normed spaces where Schauder bases provide a manageable, convergent representation aligned with topology.
Existence and Uniqueness Conditions
A Hamel basis exists in every vector space over a field, providing a unique representation of each vector as a finite linear combination of basis elements, but it is typically non-constructive and often uncountable in infinite-dimensional spaces. In contrast, a Schauder basis exists only in certain Banach spaces, allowing unique representation of vectors as countable infinite series converging in norm, which depends critically on the space's topology. Uniqueness of a Hamel basis is guaranteed up to linear isomorphism without additional structure, while Schauder bases' uniqueness and existence rely on geometric and topological properties of the underlying Banach space.
Examples: Hamel Basis in Finite and Infinite Dimensions
A Hamel basis in finite-dimensional vector spaces corresponds to a standard basis, such as the canonical basis in \(\mathbb{R}^n\), where every vector is a finite linear combination of basis vectors. In infinite-dimensional spaces like \(\ell^2\), a Hamel basis exists but is non-constructive and uncountable, making explicit examples impractical. In contrast, Schauder bases in infinite-dimensional Banach spaces, such as the sequence of unit vectors in \(\ell^p\) spaces, allow every element to be represented as a countable convergent series, facilitating computation and analysis.
Examples: Schauder Basis in Functional Analysis
A Schauder basis in functional analysis provides an example where every element in a Banach space can be uniquely expressed as a convergent infinite linear combination of basis vectors, unlike a Hamel basis which allows only finite linear combinations. Classic examples include the sequence space \( \ell^p \) ( \( 1 \leq p < \infty \) ) with the canonical unit vectors forming a Schauder basis and the space \( C[0,1] \) where the sequence of Chebyshev polynomials or the Haar system serve as Schauder bases. These bases illustrate the practical use of Schauder bases in approximating functions and solving differential equations, emphasizing their importance over Hamel bases in infinite-dimensional spaces.
Applications in Linear Algebra and Analysis
Hamel bases provide a foundation for vector spaces in linear algebra through finite linear combinations, essential for understanding vector space dimension and linear independence in finite-dimensional spaces. Schauder bases extend these concepts into infinite-dimensional Banach spaces, enabling approximation of vectors by convergent infinite series, crucial for functional analysis and operator theory. Applications of Hamel bases are primarily theoretical due to their non-constructive nature, while Schauder bases find practical use in numerical analysis, signal processing, and solving differential equations.
Summary: Choosing Between Hamel and Schauder Bases
A Hamel basis provides a unique, algebraic representation of every vector in a vector space through finite linear combinations, essential for pure algebra and finite-dimensional analysis. A Schauder basis offers infinite, convergent series expansions in topological vector spaces, making it fundamental for functional analysis and spaces like Banach or Hilbert spaces. Selecting between a Hamel basis and a Schauder basis depends on whether algebraic structure or topological convergence properties are prioritized in the study or application.
Hamel basis Infographic
 libterm.com
libterm.com