Continuous points are crucial in mathematics and computer graphics for representing uninterrupted data or curves without breaks. Understanding how continuous points function helps improve precision in modeling and ensures smooth transitions in visual designs. Explore the full article to deepen your knowledge of continuous points and their practical applications in various fields.
Table of Comparison
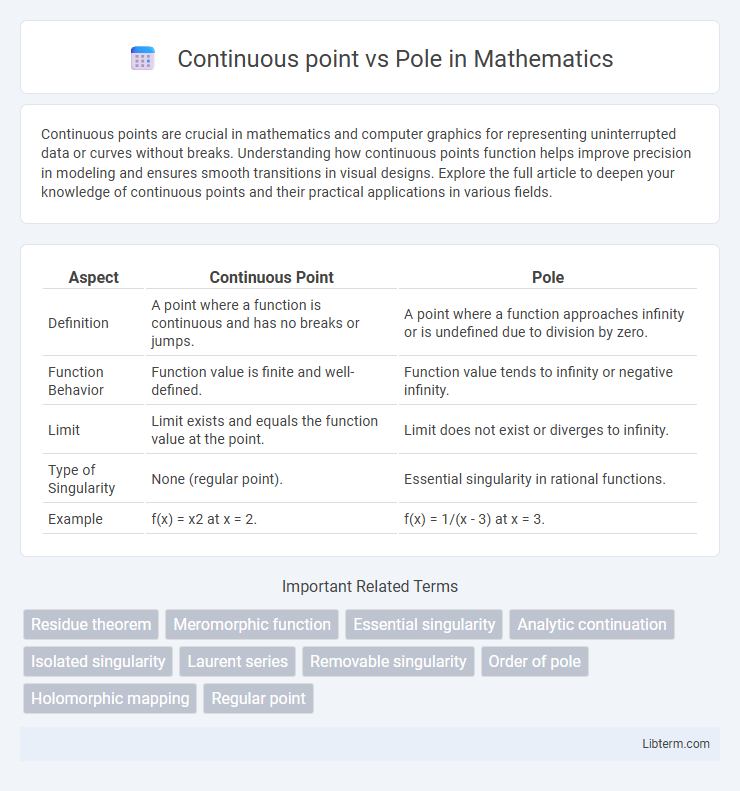
| Aspect | Continuous Point | Pole |
|---|---|---|
| Definition | A point where a function is continuous and has no breaks or jumps. | A point where a function approaches infinity or is undefined due to division by zero. |
| Function Behavior | Function value is finite and well-defined. | Function value tends to infinity or negative infinity. |
| Limit | Limit exists and equals the function value at the point. | Limit does not exist or diverges to infinity. |
| Type of Singularity | None (regular point). | Essential singularity in rational functions. |
| Example | f(x) = x2 at x = 2. | f(x) = 1/(x - 3) at x = 3. |
Introduction to Continuous Point and Pole
A continuous point in complex analysis is a point in the domain where a function is continuous and well-defined without any singularities. A pole, on the other hand, is a specific type of isolated singularity where a function's values approach infinity as the input approaches the pole. Understanding the distinction between continuous points and poles is essential for analyzing the behavior of complex functions and their singularities.
Fundamental Differences Between Continuous Point and Pole
Continuous points represent locations in a field where a function remains well-defined and smooth, while poles are singularities where the function's value approaches infinity. Continuous points exhibit finite values and maintain continuity in a complex plane, whereas poles cause disruption in analyticity due to their infinite or undefined behavior. Understanding this fundamental difference is crucial for complex analysis, as it affects residue calculations and contour integrations around singular points.
Mathematical Definitions: Continuous Point vs Pole
A continuous point in mathematics refers to a location on a function's domain where the function is well-defined and its limit equals the function value, ensuring no breaks or jumps. A pole, in contrast, is a type of singularity where a function's value tends to infinity as the variable approaches that point, typically characterized by a denominator approaching zero in rational functions. Understanding these definitions is crucial for analyzing function behavior in complex analysis and calculus.
Visualizing Continuous Points and Poles in Complex Analysis
Continuous points in complex analysis represent locations where a complex function behaves smoothly without disruptions, essential for understanding function continuity. Poles are specific types of singularities where a function's value approaches infinity, crucial for identifying function behavior near these points. Visualizing continuous points and poles often involves plotting complex functions on the complex plane using color-coded magnitude and phase diagrams to clearly differentiate smooth regions from singularities.
Criteria for Identifying Continuous Points and Poles
Continuous points are identified by analyzing a function's behavior where the limit exists and matches the function value, ensuring no interruption or jump at that point. Poles are characterized by singularities where the function approaches infinity, often detected through limits that diverge or exhibit non-removable discontinuities. Key criteria include evaluating the limit existence for continuity and examining the order and nature of the singularity to distinguish poles from other discontinuities.
Examples Illustrating Continuous Points and Poles
A continuous point in a complex function, such as f(z) = z^2, is where the function remains well-defined and smooth, like at z = 1, where f(1) = 1. In contrast, a pole represents a type of singularity where a function's value approaches infinity, exemplified by f(z) = 1/(z-2), which has a pole at z = 2. Continuous points are typical in polynomial and analytic functions, while poles often occur in rational functions and are crucial in residue calculus.
Role of Continuous Points and Poles in Function Analysis
Continuous points in function analysis represent locations where a function maintains stability and smooth behavior without interruption or gaps, crucial for ensuring predictability and integrability. Poles indicate points of singularity where the function approaches infinity, playing a significant role in understanding the function's behavior and asymptotic limits near those points. Analyzing the distribution and nature of continuous points and poles helps in characterizing complex functions, particularly in complex analysis and signal processing applications.
Applications in Engineering and Physics
Continuous points, defined as locations where a function or field remains uninterrupted and differentiable, are crucial in engineering for modeling stress and strain distributions in materials, ensuring accurate finite element analysis. Poles, representing singularities where functions approach infinity, are essential in physics for understanding phenomena such as electromagnetic fields around charged particles and resonance behavior in dynamic systems. Distinguishing between continuous points and poles enables precise simulation of physical systems and optimization of engineering designs by addressing stability and boundary conditions.
Common Misconceptions About Continuous Point and Pole
Continuous points and poles are often confused, but a continuous point refers to a location on the complex plane where a function is continuous, while a pole is a type of singularity where a function's value approaches infinity. A common misconception is that continuous points cannot be associated with any kind of singular behavior, but continuity does not preclude subtle function behavior near such points. Poles are mistakenly thought to be isolated discontinuities, though they are specific isolated singularities characterized by the function's unbounded growth rate near that point.
Summary and Key Takeaways
Continuous points represent a set of values with no gaps, often used in calculus and real analysis to describe smooth curves or functions. Poles are isolated singularities in complex analysis where a function's value approaches infinity. Understanding the distinction aids in analyzing function behavior, particularly in determining continuity, limits, and the classification of singularities in mathematical and engineering contexts.
Continuous point Infographic
 libterm.com
libterm.com