A semigroup is a fundamental algebraic structure consisting of a set equipped with an associative binary operation, meaning the grouping of operations does not affect the outcome. Understanding semigroups is essential for deeper insights into abstract algebra, computer science, and automata theory. Explore the rest of the article to discover how semigroups apply to your mathematical and computational problems.
Table of Comparison
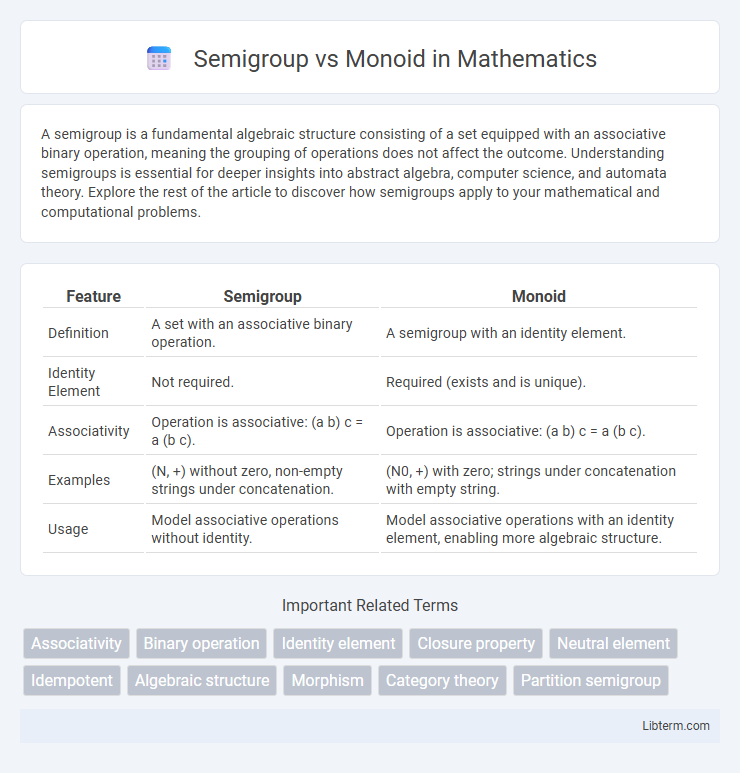
| Feature | Semigroup | Monoid |
|---|---|---|
| Definition | A set with an associative binary operation. | A semigroup with an identity element. |
| Identity Element | Not required. | Required (exists and is unique). |
| Associativity | Operation is associative: (a b) c = a (b c). | Operation is associative: (a b) c = a (b c). |
| Examples | (N, +) without zero, non-empty strings under concatenation. | (N0, +) with zero; strings under concatenation with empty string. |
| Usage | Model associative operations without identity. | Model associative operations with an identity element, enabling more algebraic structure. |
Introduction to Algebraic Structures
A semigroup is an algebraic structure consisting of a set equipped with an associative binary operation, allowing the combination of any two elements within the set. A monoid extends this structure by including an identity element that acts as a neutral element under the operation, providing a foundation for more complex algebraic systems. These fundamental constructs are essential in abstract algebra, underpinning operations in computer science, formal languages, and category theory.
What is a Semigroup?
A Semigroup is an algebraic structure consisting of a set equipped with an associative binary operation, meaning the operation combines any two elements to form another element within the same set. Unlike Monoids, Semigroups do not require an identity element for the operation. This property makes Semigroups foundational in abstract algebra and functional programming, where associative operations are essential for combining data structures or functions.
What is a Monoid?
A monoid is an algebraic structure consisting of a set equipped with an associative binary operation and an identity element that leaves other elements unchanged when combined. Unlike a semigroup, which requires only associativity, a monoid must include this identity element to satisfy completeness in composition. Monoids are fundamental in abstract algebra and computer science, underpinning structures such as strings under concatenation with the empty string as the identity.
Defining Operations: Semigroup vs Monoid
A semigroup is defined by a single associative binary operation, meaning the operation combines any two elements of the set and the grouping of operations does not affect the result. A monoid extends a semigroup by including an identity element that, when combined with any element in the set, leaves the element unchanged. The defining operations distinguish semigroups by the absence of an identity element, whereas monoids require both associativity and the presence of this identity element.
Identity Element: The Key Difference
A semigroup is an algebraic structure consisting of a set equipped with an associative binary operation, but it does not require the presence of an identity element. In contrast, a monoid extends the semigroup by including an identity element, which acts as a neutral element for the operation, satisfying the property that combining it with any element of the set leaves that element unchanged. This identity element is the key distinction that enables monoids to support additional algebraic properties and operations, such as defining invertible elements and facilitating category theory applications.
Mathematical Properties Compared
A semigroup consists of a set equipped with an associative binary operation, ensuring closure and associativity without necessarily having an identity element. A monoid extends a semigroup by including an identity element that acts as a neutral element for the operation, satisfying the condition e * a = a * e = a for all elements a in the set. The presence of this identity element distinguishes monoids from semigroups, enabling additional algebraic structures and functional applications.
Real-World Examples of Semigroups
Semigroups appear in real-world contexts such as string concatenation in programming, where combining sequences follows an associative operation without requiring an identity element. Another example is the merging of logs or event streams, where order-preserving aggregation forms a semigroup structure. Financial transactions aggregating total amounts also illustrate semigroups, as they rely on associative addition but may lack a neutral starting element.
Real-World Applications of Monoids
Monoids find extensive real-world applications in computer science, particularly in parallel and distributed computing where their associative binary operation and identity element enable efficient aggregation of data across multiple processors. In functional programming, monoids streamline the design of composable data transformations and folding operations on collections, ensuring predictable and reusable code patterns. Database systems leverage monoidal structures for consistent merging of query results and incremental updates, enhancing performance and reliability.
Relationship Between Semigroups and Monoids
A monoid is an extension of a semigroup characterized by the presence of an identity element that leaves other elements unchanged under the binary operation. Every monoid inherently forms a semigroup because it satisfies associativity, but not every semigroup qualifies as a monoid due to the potential absence of an identity element. This hierarchical relationship highlights that monoids are semigroups enriched with a neutral element, essential for algebraic structures in category theory, computer science, and abstract algebra.
Summary Table: Semigroup vs Monoid
A semigroup is an algebraic structure consisting of a set equipped with an associative binary operation, while a monoid extends a semigroup by including an identity element that leaves other elements unchanged under the operation. The summary table comparing semigroup vs monoid highlights that all monoids are semigroups, but not all semigroups qualify as monoids due to the absence of an identity element. Key properties include associativity for semigroups, with monoids requiring both associativity and the existence of an identity element, crucial in fields like computer science and abstract algebra.
Semigroup Infographic
 libterm.com
libterm.com