Immersion enhances your ability to fully engage with a new language or culture, accelerating learning through deep, hands-on experience. This method fosters natural understanding by surrounding you with relevant vocabulary, social contexts, and practical scenarios. Discover how immersion can transform your skills and confidence by exploring the full article.
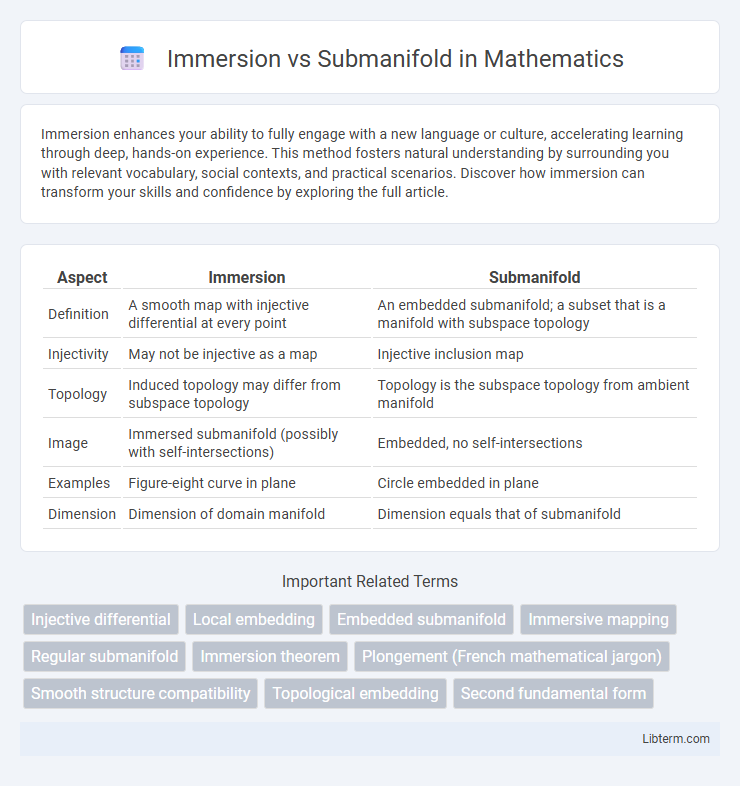
Table of Comparison
| Aspect | Immersion | Submanifold |
|---|---|---|
| Definition | A smooth map with injective differential at every point | An embedded submanifold; a subset that is a manifold with subspace topology |
| Injectivity | May not be injective as a map | Injective inclusion map |
| Topology | Induced topology may differ from subspace topology | Topology is the subspace topology from ambient manifold |
| Image | Immersed submanifold (possibly with self-intersections) | Embedded, no self-intersections |
| Examples | Figure-eight curve in plane | Circle embedded in plane |
| Dimension | Dimension of domain manifold | Dimension equals that of submanifold |
Defining Immersion and Submanifold
An immersion is a smooth map between differentiable manifolds whose differential is injective at every point, ensuring locally embedded images. A submanifold is a subset of a manifold that is itself a manifold, equipped with the induced topology and differentiable structure, typically arising as the image of an embedding or an immersion satisfying additional conditions. The key distinction lies in immersions allowing self-intersections and non-homeomorphic images, whereas submanifolds inherit a manifold structure as embedded or embedded-like subsets.
Key Differences Between Immersion and Submanifold
An immersion is a smooth map between manifolds where the differential is injective at every point, allowing the image to locally resemble the domain manifold but not necessarily be a manifold itself. A submanifold is a subset of a manifold that inherits a manifold structure making the inclusion map an embedding, ensuring both topological and differentiable properties align with the ambient manifold. Key differences include that immersions may fail to be embeddings and thus their images need not be submanifolds, whereas submanifolds are embedded and possess a manifold topology compatible with the larger space.
Mathematical Formulation of Immersion
An immersion is a smooth map \( f: M \to N \) between differentiable manifolds where the differential \( df_p: T_pM \to T_{f(p)}N \) is injective at every point \( p \in M \), ensuring the local embedding of \( M \) into \( N \) without necessarily being a homeomorphism onto its image. This condition implies that the rank of \( df_p \) equals the dimension of \( M \), establishing an injective linear map between tangent spaces. Unlike submanifolds, where \( M \) is identified as a subset of \( N \) with the subspace topology and smooth structure, immersions focus on the intrinsic property of the differential without requiring the image to be an embedded submanifold.
Conditions for a Map to Be a Submanifold
For a map to define a submanifold, it must be an immersion, meaning its differential is injective at every point in the domain. This ensures the image locally resembles Euclidean space of the same dimension as the domain, satisfying manifold structure criteria. Additionally, the image must be an embedded subset with the subspace topology induced from the codomain to qualify as a submanifold.
Examples of Immersions That Are Not Submanifolds
Immersions are smooth maps between manifolds with injective differentials, but their images need not be submanifolds due to topological or smooth structure discrepancies. A classic example is the figure-eight immersion of the circle into the plane, where the image self-intersects, preventing it from being a submanifold despite the immersion being injective on tangent spaces. Another example is the everywhere dense immersion of the real line into the torus, which is injective on differentials but whose image is not embedded as a submanifold because it fails to be a topological embedding.
Regular vs. Singular Points in Immersion
An immersion is a smooth map between manifolds whose differential is injective at every point, ensuring regular points where the tangent space dimension is preserved. Submanifolds arise as images of immersions when the immersion is also an embedding, thus avoiding singular points where the differential fails to be injective. Singular points indicate failure of immersion, characterized by the rank of the differential dropping, which distinguishes them from regular points that define the submanifold structure.
The Role of Injectivity in Submanifolds
Injectivity plays a crucial role in distinguishing submanifolds from immersions, as a submanifold requires the embedding map to be both an immersion and a homeomorphism onto its image, ensuring injectivity preserves topological and differentiable structure. Immersions allow locally injective differentials but can fail to be globally injective, causing self-intersections that prevent the underlying set from forming a submanifold. The injective nature of submanifold embeddings guarantees that the manifold structure is preserved without overlap, crucial for defining intrinsic geometric properties.
Applications in Differential Geometry
Immersion and submanifold concepts are fundamental in differential geometry for understanding manifold structures and their embeddings. Immersions allow the mapping of manifolds into higher-dimensional spaces where local injectivity of the differential ensures smooth structure preservation, critical in studying curves and surfaces. Submanifolds provide a framework for analyzing geometric properties inherited from ambient manifolds, essential in curvature analysis and the theory of Riemannian metrics.
Immersions and Submanifolds in Higher Dimensions
Immersions in higher dimensions are smooth maps between manifolds where the differential is injective at every point, allowing local embedding without requiring global injectivity. Submanifolds arise as subsets of manifolds that locally resemble Euclidean spaces of lower dimension and inherit the manifold structure, often realized as the image of an immersion with additional embedding conditions. Studying immersions and submanifolds in higher dimensions reveals distinctions in topology, such as self-intersections in immersions versus the embedded nature of submanifolds, crucial for applications in differential geometry and topology.
Summary: Choosing Between Immersion and Submanifold
Choosing between immersion and submanifold depends on the context of differentiable manifolds and their embeddings. Immersion involves a smooth map with injective differential at each point, allowing self-intersections and local embeddings, while submanifolds require an embedding with a homeomorphic image that is a subset of the ambient manifold. The decision hinges on whether a locally injective map suffices or a globally well-behaved embedding is necessary, impacting applications in geometry and topology.
Immersion Infographic
 libterm.com
libterm.com