The residue complex plays a crucial role in algebraic geometry by providing tools to analyze the local behavior of meromorphic functions and differential forms on varieties. It enables precise calculation of residues and contributes to understanding the duality theory in complex geometry. Explore the rest of the article to deepen your knowledge of residue complexes and their applications in modern mathematics.
Table of Comparison
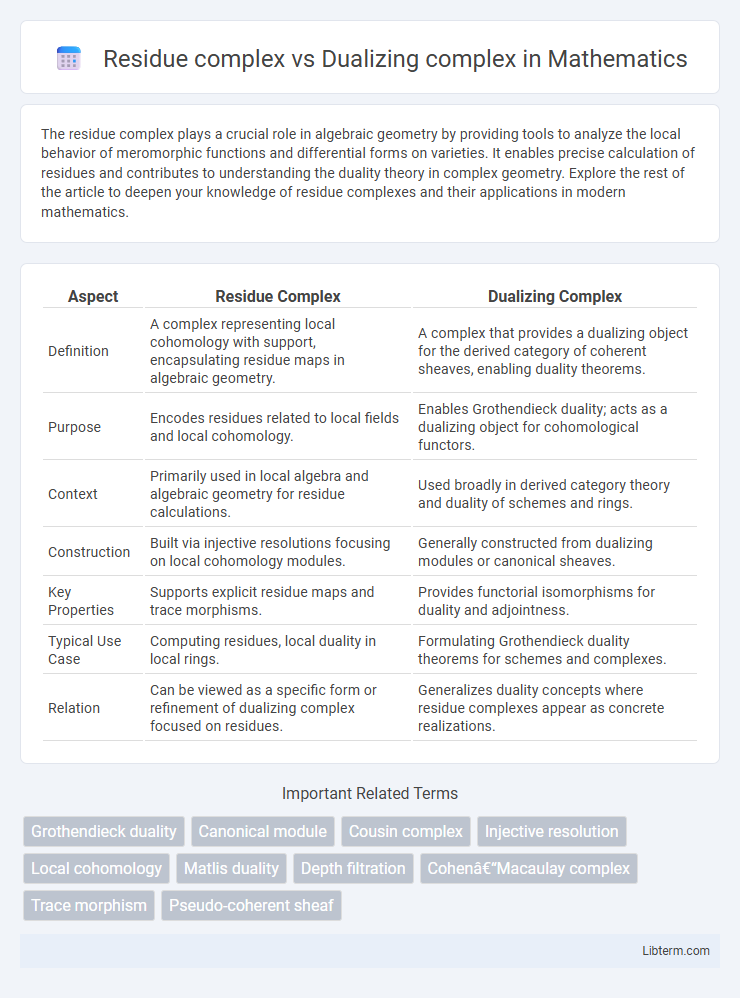
| Aspect | Residue Complex | Dualizing Complex |
|---|---|---|
| Definition | A complex representing local cohomology with support, encapsulating residue maps in algebraic geometry. | A complex that provides a dualizing object for the derived category of coherent sheaves, enabling duality theorems. |
| Purpose | Encodes residues related to local fields and local cohomology. | Enables Grothendieck duality; acts as a dualizing object for cohomological functors. |
| Context | Primarily used in local algebra and algebraic geometry for residue calculations. | Used broadly in derived category theory and duality of schemes and rings. |
| Construction | Built via injective resolutions focusing on local cohomology modules. | Generally constructed from dualizing modules or canonical sheaves. |
| Key Properties | Supports explicit residue maps and trace morphisms. | Provides functorial isomorphisms for duality and adjointness. |
| Typical Use Case | Computing residues, local duality in local rings. | Formulating Grothendieck duality theorems for schemes and complexes. |
| Relation | Can be viewed as a specific form or refinement of dualizing complex focused on residues. | Generalizes duality concepts where residue complexes appear as concrete realizations. |
Introduction to Residue Complex and Dualizing Complex
Residue complexes provide a canonical way to represent local cohomology in algebraic geometry, capturing intricate duality properties of schemes through explicit injective resolutions. Dualizing complexes serve as a fundamental tool in Grothendieck duality theory, offering a generalized notion of canonical modules that facilitate the comparison between coherent sheaves and their derived functors. Both complexes are integral in studying the duality phenomena on schemes, with residue complexes often constructed from dualizing complexes to reflect local duality at each point.
Historical Background and Development
The residue complex concept emerged from Grothendieck's work on duality theory in algebraic geometry during the 1960s, providing a tool for local cohomological calculations. Dualizing complexes were later developed to generalize and formalize duality for schemes and rings, incorporating ideas from both homological algebra and sheaf theory. This evolution marked a shift from explicit residue symbols to a more abstract, categorical framework for duality in algebraic geometry and commutative algebra.
Definitions and Core Concepts
A residue complex is a bounded complex of injective modules that provides a concrete tool for duality theory in algebraic geometry and commutative algebra, encoding local cohomological data of a ring or scheme. In contrast, a dualizing complex is an object in the derived category that generalizes the notion of a canonical module, serving as a fundamental tool for Grothendieck duality and allowing the definition of dualizing functors. Both concepts capture duality phenomena, but the residue complex is more explicit and constructed from injectives, whereas the dualizing complex is an abstract derived-category object that facilitates broader theoretical applications.
Construction Techniques
Residue complexes are constructed using a careful patching of local cohomology modules reflecting the behavior of modules over singular schemes, often relying on Cousin complexes and injective resolutions in the derived category. Dualizing complexes are constructed via derived functors that provide a global duality framework, using techniques such as Grothendieck duality and coherent sheaves to establish canonical isomorphisms in the derived category. Both constructions require intricate homological algebra, but residue complexes emphasize local residue maps and local cohomology support, while dualizing complexes focus on global duality properties and functorial adjunctions.
Key Properties and Differences
Residue complexes provide a framework to study local cohomology and duality in algebraic geometry with well-structured support on singularities, whereas dualizing complexes serve as a generalized form of canonical sheaves enabling Grothendieck duality. Key properties of residue complexes include their role in encoding local cohomological data and fine support decomposition, while dualizing complexes are characterized by their function as functorial adjoints to derived pushforward and their compatibility with Serre duality. The primary difference lies in residue complexes focusing on local duality phenomena and explicit supports, contrasting with dualizing complexes' broader applicability in deriving global duality statements in both algebraic and analytic settings.
Applications in Algebraic Geometry
Residue complexes provide a canonical tool for studying local duality and cohomological properties of schemes, enabling explicit calculations of local cohomology and dualizing functors in algebraic geometry. Dualizing complexes generalize canonical sheaves and are essential in formulating Serre duality, facilitating deep insights into the structure of singularities and duality on Cohen-Macaulay and Gorenstein schemes. Both complexes serve as foundational apparatuses for derived category methods and Grothendieck duality theory, with residue complexes offering concrete residue morphisms while dualizing complexes support broader duality frameworks in geometric and arithmetic contexts.
Role in Local Cohomology
A Residue complex provides a canonical object in derived categories that directly computes local cohomology modules with supports in a closed subset, offering explicit residue maps and duality properties. In contrast, a Dualizing complex serves as a fundamental tool for Grothendieck duality theory, enabling the identification of local cohomology with Ext-groups and establishing isomorphisms in local duality. The residue complex refines the dualizing complex structure by encoding detailed local cohomological information, making it essential for explicit calculations and residue theorems in algebraic geometry and commutative algebra.
Interactions with Grothendieck Duality
The residue complex provides a concrete model for Grothendieck duality by representing local cohomological dualizing objects explicitly, facilitating computations with local cohomology modules and residues. The dualizing complex, often defined abstractly in the derived category, serves as a global dualizing object that induces functorial isomorphisms in Grothendieck duality, allowing coherent sheaf duality statements on schemes. Interactions between residue and dualizing complexes highlight their complementary roles: residue complexes offer explicit, local descriptions, while dualizing complexes encapsulate global duality properties, both essential for understanding and applying Grothendieck duality in algebraic geometry.
Comparative Advantages and Limitations
The residue complex provides a canonical tool for local cohomology and duality theories in algebraic geometry, offering explicit calculations in regular schemes, but it is often limited to well-behaved, typically noetherian contexts. The dualizing complex extends these concepts to more general, possibly singular or non-noetherian schemes, enabling broader application of Grothendieck duality and local duality theorems, though it may lack the explicit geometric intuition present in the residue complex. While the residue complex excels in explicit computations and local-global compatibility, the dualizing complex offers greater flexibility and generality in derived category formulations, balancing computational ease against categorical abstraction.
Future Directions and Open Questions
Future directions in the study of residue complexes and dualizing complexes involve exploring their applications in non-commutative algebraic geometry and derived categories. Open questions include characterizing dualizing complexes over more general schemes and understanding the interplay between residue complexes and local cohomology in singular settings. Advances in homological methods and categorical frameworks are expected to deepen insights into these foundational tools.
Residue complex Infographic
 libterm.com
libterm.com