Almost everywhere convergence describes a sequence of functions converging at all points except for a set of measure zero, ensuring that the limit behavior is consistent across the majority of the domain. This concept is fundamental in measure theory and real analysis, particularly when studying the behavior of functions under integration or limit operations. Explore the rest of the article to understand how almost everywhere convergence impacts various mathematical fields and your analytical applications.
Table of Comparison
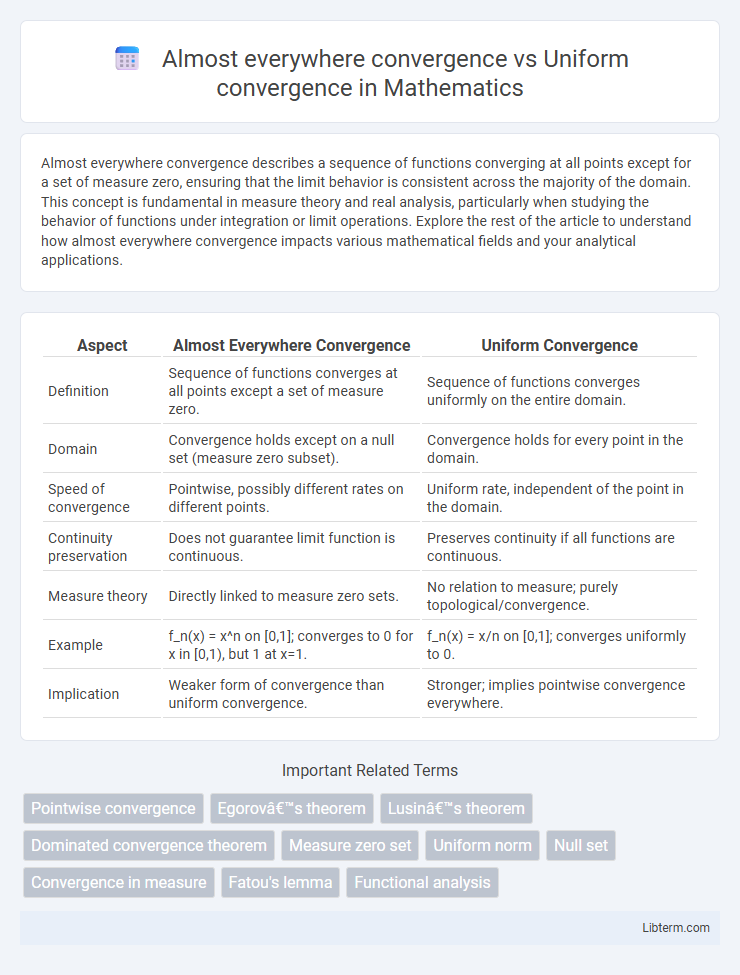
| Aspect | Almost Everywhere Convergence | Uniform Convergence |
|---|---|---|
| Definition | Sequence of functions converges at all points except a set of measure zero. | Sequence of functions converges uniformly on the entire domain. |
| Domain | Convergence holds except on a null set (measure zero subset). | Convergence holds for every point in the domain. |
| Speed of convergence | Pointwise, possibly different rates on different points. | Uniform rate, independent of the point in the domain. |
| Continuity preservation | Does not guarantee limit function is continuous. | Preserves continuity if all functions are continuous. |
| Measure theory | Directly linked to measure zero sets. | No relation to measure; purely topological/convergence. |
| Example | f_n(x) = x^n on [0,1]; converges to 0 for x in [0,1), but 1 at x=1. | f_n(x) = x/n on [0,1]; converges uniformly to 0. |
| Implication | Weaker form of convergence than uniform convergence. | Stronger; implies pointwise convergence everywhere. |
Introduction to Modes of Function Convergence
Almost everywhere convergence occurs when a sequence of functions converges pointwise for all points except a set of measure zero, making it crucial in measure theory and integration. Uniform convergence ensures that functions converge at the same rate across the entire domain, preserving continuity and allowing term-by-term integration or differentiation. Understanding these modes of function convergence is essential for analyzing function behavior in real analysis and establishing the foundation for Lebesgue integration and functional analysis.
Defining Almost Everywhere Convergence
Almost everywhere convergence occurs when a sequence of functions converges pointwise at all points except a set of measure zero, ensuring that the limit function matches the sequence almost everywhere on the domain. This concept is crucial in measure theory and Lebesgue integration, where functions may differ on negligible subsets without affecting integral properties. Unlike uniform convergence, which requires the sequence to converge uniformly across the entire domain, almost everywhere convergence permits exceptions on sets that are negligible in measure.
Understanding Uniform Convergence
Uniform convergence of a sequence of functions {f_n} to a function f ensures that for every e > 0, there exists an N such that for all n >= N, the inequality |f_n(x) - f(x)| < e holds uniformly for every x in the domain. This strong form of convergence guarantees preservation of continuity, integrability, and differentiability under the limit, unlike almost everywhere convergence, which only requires convergence at almost all points barring a set of measure zero. Understanding uniform convergence is crucial in functional analysis and approximation theory, as it provides control over the function sequence behavior across the entire domain rather than pointwise or measure-based criteria.
Key Differences Between the Two Convergences
Almost everywhere convergence occurs when a sequence of functions converges at all points except on a set of measure zero, while uniform convergence requires convergence to hold uniformly across the entire domain with no exceptions. The key difference lies in the fact that uniform convergence ensures the speed of convergence is consistent for all points, preserving continuity and integration properties, whereas almost everywhere convergence allows for varying convergence rates and does not guarantee these properties. In measure theory and functional analysis, uniform convergence is stronger and implies almost everywhere convergence, but the converse is not true, highlighting their distinct roles in analysis.
Formal Mathematical Definitions
Almost everywhere convergence of a sequence of functions {f_n} to f on a measure space (X, M, m) means that m({x X : lim_{n-} f_n(x) f(x)}) = 0, indicating convergence holds for all points except a set of measure zero. Uniform convergence requires that for every e > 0, there exists N such that for all n >= N and all x X, |f_n(x) - f(x)| < e, implying convergence is independent of x and uniformly controlled across the entire domain. Almost everywhere convergence is weaker than uniform convergence, as it permits exceptions on a null set, whereas uniform convergence demands simultaneous closeness everywhere.
Examples Illustrating Each Convergence Type
Almost everywhere convergence occurs when a sequence of functions converges at every point except on a set of measure zero, exemplified by the sequence f_n(x) = x^n on the interval [0,1), converging pointwise to a function that is zero on [0,1) and one at x=1, with convergence failing at a single point. Uniform convergence requires the functions to converge to the limit function uniformly over the entire domain, demonstrated by f_n(x) = x/n on [0,1], where the difference |f_n(x) - 0| = x/n is bounded by 1/n for all x, ensuring a uniform rate of convergence. Differentiating between these types highlights that almost everywhere convergence addresses pointwise behavior except on negligible sets, whereas uniform convergence imposes strict uniformity in the rate of convergence across the domain.
Implications in Analysis and Integration
Almost everywhere convergence ensures that a sequence of functions converges at all points except a set of measure zero, which is crucial for applying the Lebesgue Dominated Convergence Theorem in integration theory. Uniform convergence guarantees convergence at every point uniformly, allowing term-by-term integration and differentiation, thus preserving continuity and integrability. In analysis, uniform convergence implies almost everywhere convergence, but the converse is not true, affecting the interchangeability of limits and integrals.
Common Misconceptions and Pitfalls
Almost everywhere convergence and uniform convergence both describe how sequences of functions approach a limit function but differ significantly in their requirements and implications. A common misconception is assuming that almost everywhere convergence implies uniform convergence, which overlooks that the convergence can fail on sets of measure zero without being uniform. Another pitfall is neglecting the impact of the mode of convergence on interchange of limits and integrals, where uniform convergence ensures valid limit operations, whereas almost everywhere convergence does not guarantee this.
Applications in Real-world Mathematical Problems
Almost everywhere convergence is crucial in probabilistic models and signal processing where functions may converge except on negligible sets, ensuring stability of solutions despite minor irregularities. Uniform convergence is vital in numerical analysis and optimization, guaranteeing consistent approximation quality across entire domains, which supports error estimation and reliable algorithm performance. Both convergence types enable robust modeling and analysis in fields like finance, engineering, and physics by balancing precision and practical computability.
Summary and Key Takeaways
Almost everywhere convergence occurs when a sequence of functions converges at all points except on a set of measure zero, emphasizing pointwise behavior with negligible exceptions. Uniform convergence ensures that the sequence converges simultaneously at the same rate across the entire domain, providing stronger continuity and integrability properties. Key takeaways highlight that uniform convergence guarantees preservation of continuity and integrals, while almost everywhere convergence is sufficient for many measure-theoretic applications but lacks uniform control.
Almost everywhere convergence Infographic
 libterm.com
libterm.com