Coinciding events often reveal unexpected connections that can deepen your understanding of complex situations. Recognizing these overlaps can enhance decision-making and highlight patterns you might have missed. Explore the rest of the article to uncover how coinciding factors influence outcomes in various contexts.
Table of Comparison
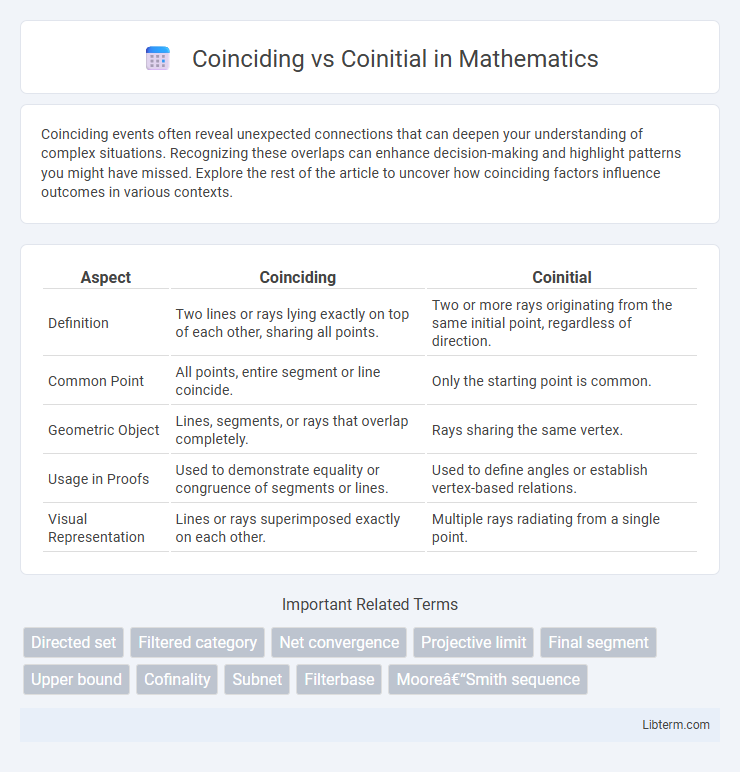
| Aspect | Coinciding | Coinitial |
|---|---|---|
| Definition | Two lines or rays lying exactly on top of each other, sharing all points. | Two or more rays originating from the same initial point, regardless of direction. |
| Common Point | All points, entire segment or line coincide. | Only the starting point is common. |
| Geometric Object | Lines, segments, or rays that overlap completely. | Rays sharing the same vertex. |
| Usage in Proofs | Used to demonstrate equality or congruence of segments or lines. | Used to define angles or establish vertex-based relations. |
| Visual Representation | Lines or rays superimposed exactly on each other. | Multiple rays radiating from a single point. |
Introduction to Coinciding and Coinitial
Coinciding refers to two or more events, points, or lines occurring at the same time or occupying the same position simultaneously in space or time. Coinitial specifically describes two or more rays or line segments sharing the same initial point or origin, emphasizing their common starting point rather than their entire length. Understanding the distinction between coinciding and coinitial is essential in geometry for accurately describing spatial relationships and intersections.
Definitions: Coinciding vs Coinitial
Coinciding refers to two or more events or elements occurring at the same time or occupying the same position in space, emphasizing simultaneity or overlap. Coinitial specifically describes two or more sequences or rays sharing the same initial point or origin, highlighting a common starting position rather than overall overlap. Understanding the distinction between coinciding as simultaneous occurrence and coinitial as sharing an initial point is crucial in fields like mathematics and physics.
Key Differences Between Coinciding and Coinitial
Coinciding refers to two or more events or entities occupying the same position or time simultaneously, emphasizing exact overlap in location or occurrence. Coinitial specifically denotes having the same starting point or origin, usually in a temporal or spatial context, highlighting a shared beginning rather than continuous overlap. The key difference lies in coinciding involving full concurrence in position or time, while coinitial focuses solely on the point of commencement.
Mathematical Contexts: Coincidence and Coinitiality
Coinciding in mathematical contexts refers to two or more geometric figures or points occupying the same position or having identical coordinates, indicating exact overlap or congruence. Coinitiality describes multiple line segments or functions sharing the same initial point or starting value, emphasizing a common origin rather than complete overlap. Understanding the distinction between coincidence (complete alignment) and coinitiality (shared starting point) is crucial in geometry, vector analysis, and function theory.
Coinciding in Topology and Algebra
Coinciding in topology refers to two functions or sequences sharing the same limit or value at a particular point, emphasizing their identical behavior within a neighborhood. In algebra, coinciding often involves elements or structures that match under specific operations or mappings, such as coinciding homomorphisms producing equal outputs for every input. This concept is fundamental in studying continuity, convergence, and morphism properties in both fields.
Coinitial in Category Theory
Coinitial functors in category theory preserve colimits by ensuring that the comma category under every object is connected and non-empty, which implies a strong form of "coverage" compared to coinciding morphisms that simply agree or overlap. This property allows coinitial functors to reflect universal constructions accurately, making them essential in the analysis of limits, colimits, and the behavior of diagrams in categories. Understanding coinciding morphisms is useful for comparing objects or morphisms, but coinitial functors provide deeper insights into the structural relationships and categorical completeness.
Practical Examples of Coinciding
Coinciding events occur simultaneously but independently, such as two separate trains arriving at the station at the same time, whereas coinitial events start together from the same initial point, like two runners beginning a race simultaneously. In practical contexts, coinciding dates on calendars denote events that overlap in time without causal relation, exemplifying occurrences that share temporal alignment. Understanding these distinctions aids in scheduling and analyzing temporal data accurately in fields like project management and logistics.
Practical Examples of Coinitial
Coinitial refers to two or more line segments or rays sharing the same starting point, such as rays OA and OB originating from point O in geometry, illustrating their common endpoint. Practical examples of coinitial rays include the hands of a clock at 12:00, where both hands start from the clock's center, and adjacent walls meeting at a corner, which form coinitial angles. Understanding coinitial is essential in topics like angle measurement and vector analysis, emphasizing the shared initial point for accurate geometric interpretations.
Common Misconceptions and Errors
Coinciding refers to two or more events or objects occurring at the exact same time or place, while coinitial specifically describes sharing the same starting point in time or space. A common misconception is that coinitial events must also coincide throughout their entire duration, but coinitiality only guarantees a shared beginning. Misinterpreting coinitial as coinciding can lead to errors in scheduling, project planning, and mathematical contexts where the distinction impacts outcome accuracy.
Summary and Applications
Coinciding refers to two or more events or points occurring at the exact same position or time, while coinitial specifically describes multiple events or elements sharing the same starting point. In mathematics and physics, distinguishing between coinciding and coinitial helps analyze vectors, timelines, and geometric constructions with precision. Applications include signal synchronization, vector analysis in coordinate systems, and event planning where accurate alignment or simultaneous initiation is critical.
Coinciding Infographic
 libterm.com
libterm.com