A bijection is a one-to-one correspondence between elements of two sets, ensuring every element in one set pairs with a unique element in the other. This concept is fundamental in mathematics for defining equivalence and invertible functions. Discover how understanding bijections can enhance your grasp of mathematical relationships by exploring the full article.
Table of Comparison
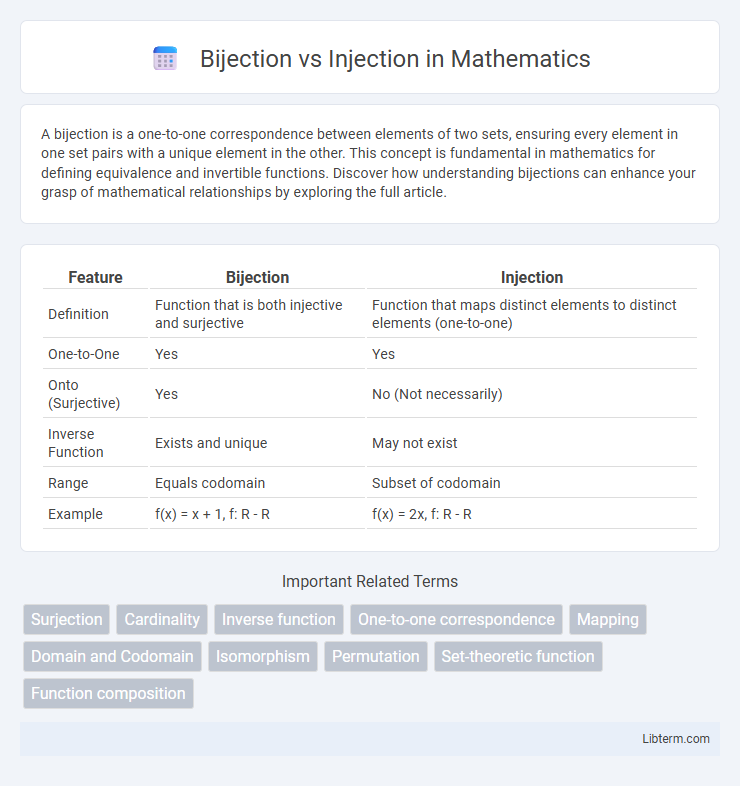
| Feature | Bijection | Injection |
|---|---|---|
| Definition | Function that is both injective and surjective | Function that maps distinct elements to distinct elements (one-to-one) |
| One-to-One | Yes | Yes |
| Onto (Surjective) | Yes | No (Not necessarily) |
| Inverse Function | Exists and unique | May not exist |
| Range | Equals codomain | Subset of codomain |
| Example | f(x) = x + 1, f: R - R | f(x) = 2x, f: R - R |
Introduction to Bijection and Injection
Bijection and injection are fundamental concepts in set theory and mathematical functions. An injection, or one-to-one function, maps each element of the domain to a unique element in the codomain, ensuring no two different inputs share the same output. In contrast, a bijection is a function that is both injective and surjective, guaranteeing a perfect one-to-one correspondence between elements of the domain and codomain, enabling invertibility.
Defining Injection: One-to-One Functions
An injection, or one-to-one function, maps each element of the domain to a unique element in the codomain, ensuring no two distinct inputs share the same output. This property guarantees that the function is reversible on its image, meaning an inverse function can be defined for all outputs in the range of the injection. In contrast to bijections, injections do not require every element of the codomain to be mapped, only that the mapping is uniquely assigned.
Understanding Bijection: One-to-One and Onto
A bijection is a function that is both one-to-one (injective) and onto (surjective), ensuring every element in the codomain is uniquely paired with an element in the domain. This guarantees that no two distinct inputs map to the same output and every possible output is covered. Understanding bijections is fundamental in fields like set theory and combinatorics for establishing one-to-one correspondences between sets.
Key Differences Between Injection and Bijection
Injection, or one-to-one function, maps each element of the domain to a unique element in the codomain, ensuring no two distinct inputs share the same output. Bijection combines injection and surjection, meaning every element in the codomain is mapped by exactly one element in the domain, establishing a perfect one-to-one correspondence. The key difference lies in surjectivity: injections do not require every codomain element to be mapped, whereas bijections guarantee a complete and reversible mapping between domain and codomain.
Visual Representation of Functions
Visual representation of functions helps clarify differences between bijection and injection by illustrating mapping behavior. Injection shows each element in the domain linked to a unique element in the codomain, but some codomain elements may remain unmapped, reflecting one-to-one but not onto characteristics. Bijection depicts a perfect pairing where every domain element maps uniquely to a codomain element, covering the entire codomain, embodying both one-to-one and onto properties.
Mathematical Notation and Formal Definitions
A function \( f: A \to B \) is an injection (one-to-one) if for all \( x_1, x_2 \in A \), \( f(x_1) = f(x_2) \implies x_1 = x_2 \), ensuring distinct elements in the domain map to distinct elements in the codomain. A bijection is a function \( f: A \to B \) that is both injective and surjective, meaning for every \( b \in B \), there exists a unique \( a \in A \) such that \( f(a) = b \), establishing a one-to-one correspondence. The notation \( f: A \leftrightarrow B \) often denotes bijections, highlighting their invertibility and equivalence between sets in cardinality.
Real-World Examples of Injection and Bijection
Injection, or one-to-one function, occurs when each input maps to a unique output, such as assigning each student ID to a specific student in a university database. Bijection combines injection and surjection, establishing a perfect pairing where every element in one set matches exactly one element in another, like a unique employee badge number corresponding directly to an employee. These concepts help clarify data organization in systems where uniqueness and completeness of mappings are essential for accuracy and retrieval.
Importance in Set Theory and Mathematics
Bijections establish a perfect one-to-one correspondence between sets, ensuring both injectivity and surjectivity, which is essential for proving equivalence in cardinality and structure in set theory. Injections, while only guaranteeing one-to-one mapping without covering the entire target set, provide crucial tools for embedding subsets and demonstrating subset relations. Understanding these functions aids in defining isomorphisms and analyzing complex mathematical structures.
Common Applications and Use Cases
Bijections are essential in cryptography for creating reversible encryption algorithms where each plaintext maps uniquely to a ciphertext, ensuring data security and integrity. In database management, injections are commonly used for partial mappings, such as indexing and key constraints, where uniqueness of mapping only from the domain side is required. Both functions play critical roles in algorithm design, data compression, and error detection codes by defining precise input-output relationships.
Summary and Comparative Analysis
A bijection is a function that is both injective (one-to-one) and surjective (onto), mapping each element of the domain to a unique element in the codomain with perfect pairing. An injection ensures uniqueness in mapping but may not cover the entire codomain, while a bijection guarantees a complete pairing of domain and codomain elements. Comparing both, bijections are invertible functions, allowing an inverse function to exist, whereas injections lack this property without surjectivity.
Bijection Infographic
 libterm.com
libterm.com