Context-free languages form the foundation of many programming languages and parsers, characterized by grammars where production rules replace single non-terminals with strings of terminals and non-terminals. These languages are recognized by pushdown automata, enabling efficient parsing techniques essential for compiler design and syntax analysis. Explore the rest of this article to deepen your understanding of context-free languages and their practical applications.
Table of Comparison
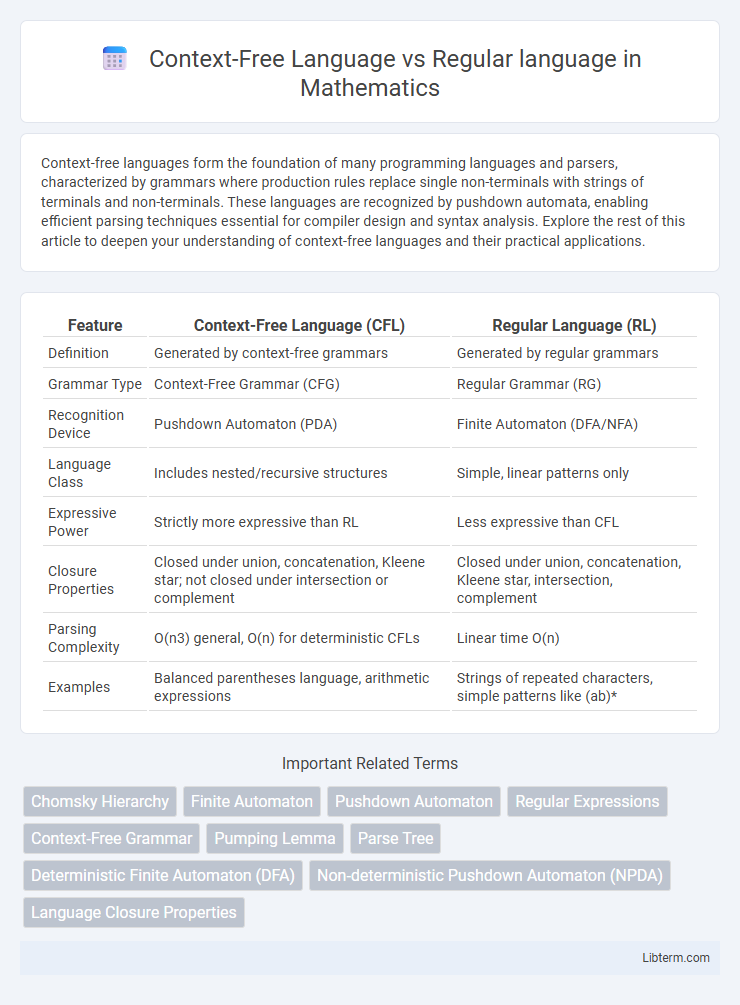
| Feature | Context-Free Language (CFL) | Regular Language (RL) |
|---|---|---|
| Definition | Generated by context-free grammars | Generated by regular grammars |
| Grammar Type | Context-Free Grammar (CFG) | Regular Grammar (RG) |
| Recognition Device | Pushdown Automaton (PDA) | Finite Automaton (DFA/NFA) |
| Language Class | Includes nested/recursive structures | Simple, linear patterns only |
| Expressive Power | Strictly more expressive than RL | Less expressive than CFL |
| Closure Properties | Closed under union, concatenation, Kleene star; not closed under intersection or complement | Closed under union, concatenation, Kleene star, intersection, complement |
| Parsing Complexity | O(n3) general, O(n) for deterministic CFLs | Linear time O(n) |
| Examples | Balanced parentheses language, arithmetic expressions | Strings of repeated characters, simple patterns like (ab)* |
Introduction to Formal Languages
Context-Free Languages (CFLs) are generated by context-free grammars and can represent nested structures such as balanced parentheses, which Regular Languages cannot. Regular Languages are recognized by finite automata and described by regular expressions, suitable for simple pattern matching without recursion. In formal language theory, understanding the distinction between CFLs and Regular Languages is essential for parsing and designing compilers, as CFLs offer greater expressive power for syntax analysis.
Defining Regular Languages
Regular languages are defined by their ability to be recognized by finite automata and described using regular expressions, characterized by closure under union, concatenation, and Kleene star operations. They represent simpler patterns compared to context-free languages, which require context-free grammars and pushdown automata for recognition. Regular languages are limited in expressing nested structures, making them suitable for lexical analysis and pattern matching tasks.
Defining Context-Free Languages
Context-free languages (CFLs) are defined by context-free grammars (CFGs) where production rules replace a single non-terminal symbol with a string of terminals and non-terminals, enabling hierarchical structure representation. Unlike regular languages, which are recognized by finite automata and described by regular expressions, CFLs can capture nested and recursive patterns essential for programming languages and natural language syntax. The defining feature of context-free languages is their ability to handle an unbounded number of nested constructs, such as matching parentheses, which regular languages cannot represent.
Key Differences Between Regular and Context-Free Languages
Regular languages are recognized by finite automata and described by regular expressions, characterized by limited memory and inability to handle nested structures. Context-free languages, generated by context-free grammars and recognized by pushdown automata, allow for hierarchical nesting and recursion, such as balanced parentheses. The key difference lies in expressiveness: context-free languages can represent patterns with nested dependencies, while regular languages cannot, making context-free languages strictly more powerful in language representation.
Examples of Regular Languages
Regular languages include examples such as strings consisting of a repeated single character (e.g., a^n where n >= 0), finite languages like {cat, dog, bird}, and patterns describable by regular expressions such as (0|1)* representing all binary strings. These languages can be recognized by deterministic or nondeterministic finite automata, showcasing their limited computational power compared to context-free languages. Regular languages are closed under union, concatenation, and Kleene star operations, making them essential for lexical analysis and pattern matching tasks.
Examples of Context-Free Languages
Context-free languages include classic examples such as balanced parentheses, arithmetic expressions, and palindromes, which cannot be represented by regular languages due to their need for nested or recursive structures. The language of balanced parentheses, {( )^n | n >= 0}, requires a context-free grammar because it involves matching pairs at varying depths, a feature regular languages fail to capture. Palindromes over a given alphabet demonstrate context-free characteristics since the structure depends on symmetry about the center, which cannot be processed by finite automata alone.
Closure Properties Comparison
Context-Free Languages (CFLs) are closed under union, concatenation, and Kleene star, but not closed under intersection or complement, whereas Regular Languages (RLs) demonstrate closure properties under union, intersection, concatenation, Kleene star, and complement. This distinction highlights RLs' more robust closure properties due to their simpler structure and finite automata representation. CFLs' lack of closure under intersection and complement stems from the complexity of context-free grammars and pushdown automata, limiting their algebraic manipulation compared to regular languages.
Applications in Computer Science
Regular languages are widely used in lexical analysis, pattern matching, and text searching due to their efficient recognition by finite automata. Context-free languages play a crucial role in programming language design, enabling the parsing of nested structures like parentheses and block scopes through pushdown automata. Both form the theoretical foundation for compiler construction, enabling syntactic validation and tokenization processes that translate high-level code into executable machine instructions.
Limitations of Regular and Context-Free Languages
Regular languages cannot handle nested structures or multiple levels of dependencies, limiting their ability to represent balanced parentheses or matching tags. Context-free languages overcome many of these limitations by allowing recursive definitions and hierarchical structures but still cannot express certain context-sensitive constraints such as cross-serial dependencies or equivalence relations between multiple substrings. Both classes are insufficient for modeling all natural language syntax due to these inherent restrictions.
Summary and Practical Implications
Context-free languages (CFLs) are more expressive than regular languages, enabling the representation of nested structures like balanced parentheses, which regular languages cannot handle due to their limited memory capacity. Regular languages are efficiently recognized by finite automata, making them ideal for simple pattern matching tasks such as lexical analysis in compilers. CFLs require pushdown automata for recognition, supporting parsing of programming languages and hierarchical data formats, crucial in compiler design and natural language processing.
Context-Free Language Infographic
 libterm.com
libterm.com