Inverse limit is a fundamental concept in category theory and algebra that allows the construction of a new object by coherently "gluing together" a family of objects indexed by a directed set. This technique captures the limiting behavior of a system in a way that preserves structural relationships, making it essential for understanding projective systems and their applications in topology and algebra. Dive into the rest of the article to explore how inverse limits play a crucial role in mathematical frameworks and your studies.
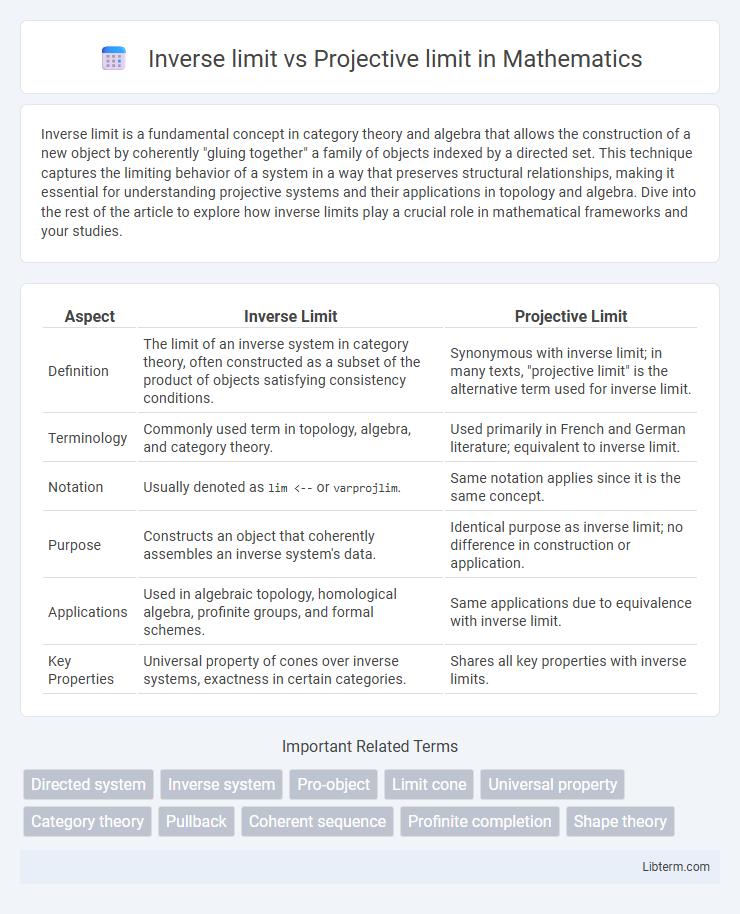
Table of Comparison
| Aspect | Inverse Limit | Projective Limit |
|---|---|---|
| Definition | The limit of an inverse system in category theory, often constructed as a subset of the product of objects satisfying consistency conditions. | Synonymous with inverse limit; in many texts, "projective limit" is the alternative term used for inverse limit. |
| Terminology | Commonly used term in topology, algebra, and category theory. | Used primarily in French and German literature; equivalent to inverse limit. |
| Notation | Usually denoted as lim <-- or varprojlim. |
Same notation applies since it is the same concept. |
| Purpose | Constructs an object that coherently assembles an inverse system's data. | Identical purpose as inverse limit; no difference in construction or application. |
| Applications | Used in algebraic topology, homological algebra, profinite groups, and formal schemes. | Same applications due to equivalence with inverse limit. |
| Key Properties | Universal property of cones over inverse systems, exactness in certain categories. | Shares all key properties with inverse limits. |
Introduction to Inverse and Projective Limits
Inverse limits and projective limits refer to the same concept in category theory, describing a way to construct objects by "limiting" an inverse system of objects and morphisms. An inverse limit is defined as the universal object that maps coherently to all objects in the inverse system, preserving the directed structure of the index set. This construction is fundamental in algebra, topology, and analysis for capturing limiting behavior of sequences of algebraic structures or topological spaces, enabling detailed study of their properties through a projective framework.
Understanding the Concept of Limits in Mathematics
The inverse limit, also known as the projective limit, is a fundamental concept in category theory and topology, describing a way to construct an object by "limiting" a sequence of related objects and morphisms directed backward. Understanding projective limits involves exploring how these limits unify structures such as groups, rings, or topological spaces through a system of compatible projections, preserving essential properties across infinite processes. This framework allows mathematicians to analyze complex structures by decomposing them into simpler components linked through inverse systems, providing crucial insights in fields like algebraic geometry and functional analysis.
Defining Inverse Limit: Key Features and Formalism
Inverse limit, also known as projective limit, is a construction in category theory and algebra capturing the universal object representing the limit of an inverse system of objects connected by morphisms. It consists of a tuple of elements from each object in the system that are compatible with the connecting morphisms, ensuring coherence across the entire inverse system. Formally, given a directed poset \(I\) and an inverse system \(\{X_i, f_{ij}\}\) where \(f_{ij}: X_j \to X_i\) for \(i \leq j\), the inverse limit \(\varprojlim X_i\) is the subset of the product \(\prod_{i \in I} X_i\) comprising elements \((x_i)_{i \in I}\) such that \(f_{ij}(x_j) = x_i\) for all \(i \leq j\).
What is a Projective Limit?
A projective limit, also known as an inverse limit, is a construction in category theory that allows one to define an object by specifying a family of objects connected by morphisms in a directed system. It captures the universal property where the limit object maps consistently to each object in the system, preserving the structure imposed by the connecting morphisms. This concept is fundamental in fields like topology, algebra, and analysis for constructing objects such as profinite groups and complete metric spaces by "limiting" along inverse sequences.
Inverse Limit vs Projective Limit: Semantic Distinctions
Inverse limit and projective limit are terms often used interchangeably in category theory and algebra, but the inverse limit specifically emphasizes the construction from a directed system of objects and morphisms indexed by a poset. The projective limit highlights the universal property that maps consistently into these objects, ensuring a unique factorization through the limit. Semantic distinctions hinge on context: inverse limit commonly refers to the process and preserving structure, while projective limit underlines the categorical universal characterization.
Topological and Algebraic Contexts of Inverse Limits
Inverse limits, also known as projective limits, provide a way to construct objects in categories like topological spaces and algebraic structures by taking limits over directed systems of objects and morphisms. In the topological context, inverse limits capture intricate structure by encoding consistency conditions across spaces with continuous bonding maps, often yielding compact or profinite spaces. Algebraically, inverse limits facilitate the study of objects such as modules, groups, or rings by assembling compatible families of finite approximations, playing a crucial role in areas like homological algebra and algebraic geometry.
Category Theory Perspective: Morphisms and Diagrams
Inverse limits and projective limits are synonymous terms in category theory, describing a universal cone over a diagram of objects and morphisms indexed by a directed poset. They capture the notion of a limit of a functor from a small category, emphasizing morphisms that commute with the connecting maps in the diagram. The construction provides a universal object that factorizes all compatible families of morphisms, essential in understanding completeness in categories.
Real-World Applications of Inverse and Projective Limits
Inverse limits and projective limits are fundamental concepts in category theory with extensive real-world applications across various scientific fields. In engineering, inverse limits model complex systems by capturing their behavior through consistent approximations at different scales, such as in signal processing and control theory. Projective limits facilitate the analysis of hierarchical data structures and large-scale networks, enabling efficient computation and robust data integration in computer science and database management.
Common Misconceptions and Clarifications
Inverse limit and projective limit refer to the same concept in category theory and algebra, often used interchangeably, leading to confusion. A common misconception is treating them as distinct constructions, whereas the projective limit is the correct formal term for the universal object defined by a projective system. Clarifying this terminology helps avoid errors in understanding inverse systems and their limits in topology, algebra, and related fields.
Summary and Further Reading on Limit Constructions
Inverse limits and projective limits refer to the same concept in category theory, describing the limit of a system of objects and morphisms indexed by a directed set, often used in topology and algebra. The inverse limit provides a way to reconstruct an object from its approximations, typically through a family of compatible projections. For further reading, foundational texts such as Mac Lane's *Categories for the Working Mathematician* and S. Willard's *General Topology* offer comprehensive discussions on limit constructions and their applications in various mathematical fields.
Inverse limit Infographic
 libterm.com
libterm.com