Rings symbolize commitment and personal style, making the choice of metal, design, and gemstone essential to reflect your unique story. Understanding the differences between gold, silver, platinum, and alternative metals ensures durability and aesthetic appeal for daily wear. Explore the rest of the article to find the perfect ring that matches your personality and occasion.
Table of Comparison
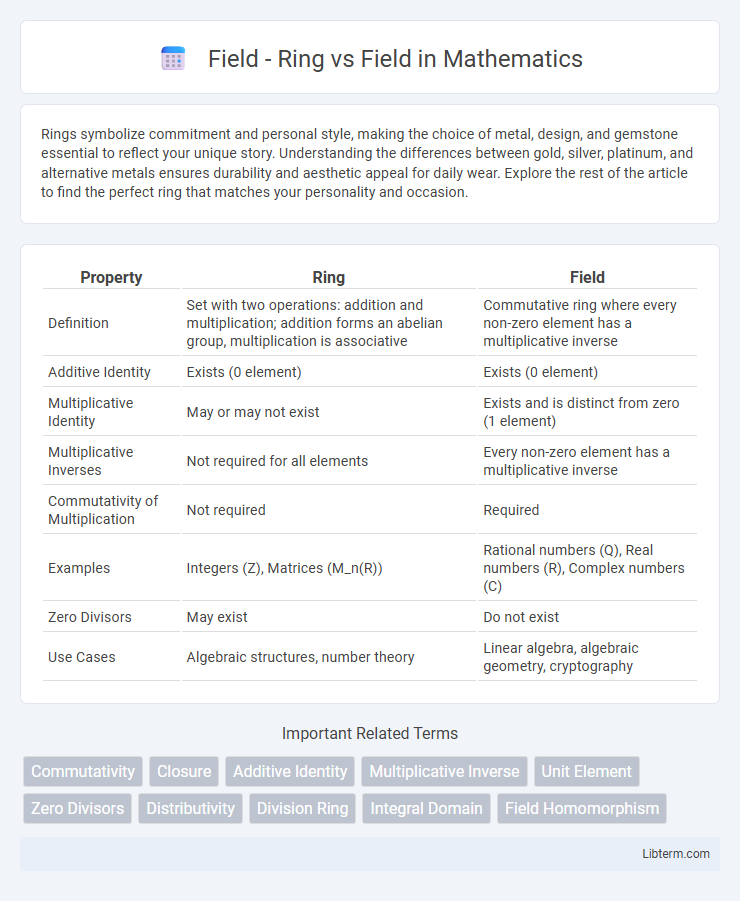
| Property | Ring | Field |
|---|---|---|
| Definition | Set with two operations: addition and multiplication; addition forms an abelian group, multiplication is associative | Commutative ring where every non-zero element has a multiplicative inverse |
| Additive Identity | Exists (0 element) | Exists (0 element) |
| Multiplicative Identity | May or may not exist | Exists and is distinct from zero (1 element) |
| Multiplicative Inverses | Not required for all elements | Every non-zero element has a multiplicative inverse |
| Commutativity of Multiplication | Not required | Required |
| Examples | Integers (Z), Matrices (M_n(R)) | Rational numbers (Q), Real numbers (R), Complex numbers (C) |
| Zero Divisors | May exist | Do not exist |
| Use Cases | Algebraic structures, number theory | Linear algebra, algebraic geometry, cryptography |
Introduction to Algebraic Structures
A field is a commutative ring with unity where every nonzero element has a multiplicative inverse, ensuring division is always possible except by zero. Rings generalize fields by allowing elements that do not have inverses, and they may lack commutativity or multiplicative identity. Understanding the distinction between rings and fields is fundamental in algebraic structures, as fields provide a framework for solving polynomial equations and enable vector space theory.
Defining Fields: Key Characteristics
Fields are algebraic structures consisting of a set equipped with two operations, addition and multiplication, satisfying properties such as commutativity, associativity, distributivity, the existence of additive and multiplicative identities, and inverses for every nonzero element. Ring structures generalize fields by relaxing the requirement for multiplicative inverses, allowing elements without inverses under multiplication, which distinguishes fields by their division capability. The defining characteristic of a field is that every nonzero element must have a multiplicative inverse, enabling division, whereas rings may lack this property and often have zero divisors.
Understanding Rings: Essential Properties
Rings are algebraic structures consisting of a set equipped with two binary operations, addition and multiplication, where addition forms an abelian group and multiplication is associative but not necessarily commutative or invertible. Fields are specialized rings where every nonzero element has a multiplicative inverse, making division always possible within the field. Understanding rings involves recognizing essential properties such as the presence of an additive identity, distributive laws, and the absence of multiplicative inverses for some elements, which differentiates them fundamentally from fields.
Core Differences Between Fields and Rings
Fields and rings are fundamental algebraic structures with distinct properties; fields require every nonzero element to have a multiplicative inverse, making division always possible, whereas rings do not. Rings allow for addition, subtraction, and multiplication but may lack multiplicative inverses for all elements, resulting in less restrictive operations. The presence of multiplicative inverses in fields ensures division forms a key operation, which is absent or limited in rings, highlighting their core algebraic difference.
Examples of Fields in Mathematics
Fields in mathematics are algebraic structures where addition, subtraction, multiplication, and division (except by zero) are well-defined and satisfy specific axioms. Examples of fields include the set of rational numbers (Q), real numbers (R), and complex numbers (C), each featuring closure, associativity, distributivity, and the existence of multiplicative inverses. In contrast, a ring like the integers (Z) lacks multiplicative inverses for every nonzero element, making it a ring but not a field.
Common Examples of Rings
Common examples of rings include the set of integers \(\mathbb{Z}\), polynomial rings like \(\mathbb{R}[x]\), and matrix rings such as \(M_n(\mathbb{R})\), each exhibiting properties like closure under addition and multiplication without requiring multiplicative inverses. Fields extend rings by ensuring every nonzero element has a multiplicative inverse, examples being the sets of rational numbers \(\mathbb{Q}\), real numbers \(\mathbb{R}\), and complex numbers \(\mathbb{C}\). The distinction highlights that while all fields are rings, not all rings qualify as fields due to the lack of divisibility and unit elements in some rings.
Field vs Ring: Structural Implications
A field is a ring with additional properties where every nonzero element has a multiplicative inverse, making division always possible except by zero. This structural difference implies that fields are inherently commutative rings with unity where ideal structure is simpler, typically allowing only trivial ideals. In contrast, rings lack multiplicative inverses for most elements, which leads to more complex behavior in their algebraic structure and ideal theory.
Applications of Fields in Science and Engineering
Fields in mathematics, such as finite fields and real number fields, play a critical role in coding theory, cryptography, and signal processing by enabling error detection and secure data transmission. Rings, while more general algebraic structures, are pivotal in materials science and quantum mechanics for modeling symmetry and particle interactions through ring theory and operator algebras. The distinction between field and ring structures influences their application scope, with fields offering invertibility needed for solving linear equations, essential in control systems and communication engineering.
Practical Uses of Rings in Mathematics
Rings play a crucial role in various branches of mathematics such as algebraic geometry, number theory, and cryptography due to their flexible structure that includes addition and multiplication but does not require multiplicative inverses. This flexibility allows rings to model polynomial functions, matrices, and integer arithmetic, providing tools for solving equations and analyzing algebraic structures where fields might be too restrictive. Practical applications of rings include coding theory, error detection, and encryption algorithms, leveraging their ability to handle modular arithmetic and complex integral domains beyond the capabilities of fields.
Choosing Between a Field and a Ring: Guidelines and Considerations
Choosing between a field and a ring depends primarily on the algebraic properties required for the application, with fields offering commutative multiplication, multiplicative inverses for every nonzero element, and more structure suitable for solving equations. Rings provide a more general framework lacking multiplicative inverses, making them ideal for studying integer-like structures, polynomials, and modules where divisibility and factorization properties are crucial. When selecting, consider whether the problem demands division (favoring fields) or only additive and multiplicative closure without division (favoring rings) to guide the decision effectively.
Field - Ring Infographic
 libterm.com
libterm.com