An equalizer shapes the sound by adjusting specific frequency bands to enhance your audio experience. Using an equalizer allows precise control over bass, midrange, and treble levels, helping tailor music or soundtracks to your preferences. Discover how to optimize your sound with our in-depth guide on equalizers.
Table of Comparison
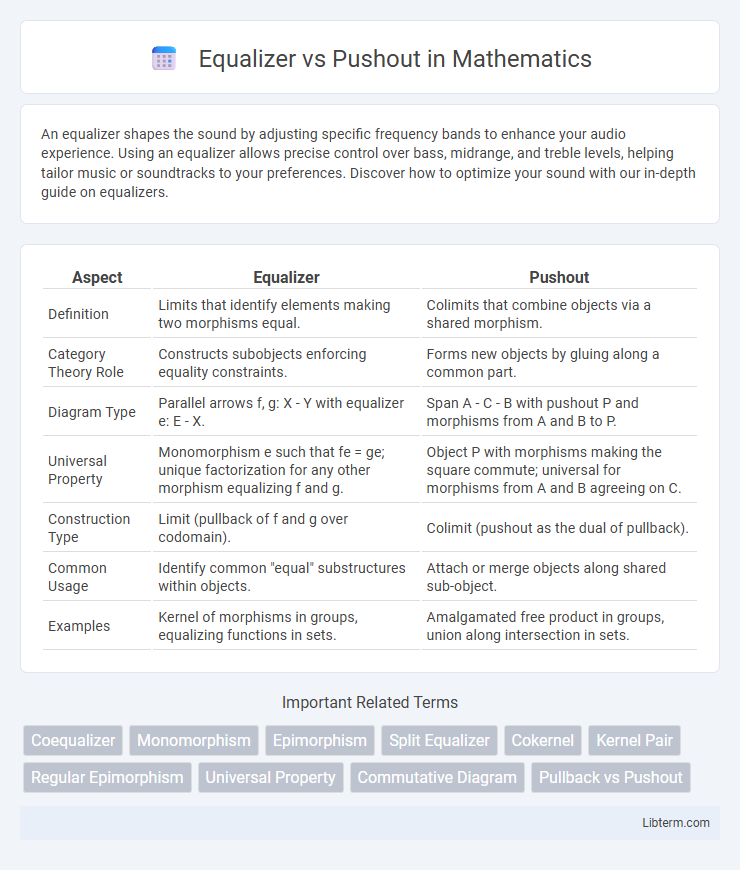
| Aspect | Equalizer | Pushout |
|---|---|---|
| Definition | Limits that identify elements making two morphisms equal. | Colimits that combine objects via a shared morphism. |
| Category Theory Role | Constructs subobjects enforcing equality constraints. | Forms new objects by gluing along a common part. |
| Diagram Type | Parallel arrows f, g: X - Y with equalizer e: E - X. | Span A - C - B with pushout P and morphisms from A and B to P. |
| Universal Property | Monomorphism e such that fe = ge; unique factorization for any other morphism equalizing f and g. | Object P with morphisms making the square commute; universal for morphisms from A and B agreeing on C. |
| Construction Type | Limit (pullback of f and g over codomain). | Colimit (pushout as the dual of pullback). |
| Common Usage | Identify common "equal" substructures within objects. | Attach or merge objects along shared sub-object. |
| Examples | Kernel of morphisms in groups, equalizing functions in sets. | Amalgamated free product in groups, union along intersection in sets. |
Introduction to Equalizer and Pushout
Equalizers and pushouts are fundamental concepts in category theory used to describe universal constructions. An equalizer identifies the largest subobject through which two parallel morphisms agree, effectively capturing their common behavior. In contrast, a pushout constructs the minimal object amalgamating two objects along a shared subobject, enabling the combination of structures while preserving their relationships.
Definition of Equalizer
An equalizer in category theory is a limit that identifies the largest subobject on which two morphisms agree, effectively "equalizing" them by capturing elements mapped identically by both morphisms. It is defined by a universal property where an object and a morphism factor through any other morphism equalizing the pair. In contrast, a pushout is a colimit constructing a new object by "pushing out" along shared morphisms, dual to the concept of an equalizer.
Definition of Pushout
Pushout is a fundamental concept in category theory representing the colimit of two morphisms with a shared domain, effectively merging objects along common parts to form a new object. It generalizes the notion of union in set theory and plays a crucial role in constructing spaces or structures by identifying elements via given maps. In contrast, an equalizer captures the limit of two morphisms by defining a subobject where these morphisms agree, focusing on equalizing elements rather than merging them.
Key Differences Between Equalizer and Pushout
Equalizer and pushout are fundamental concepts in category theory that capture dual notions of universal constructions. Equalizers identify an object that coequalizes two morphisms by selecting elements where the morphisms agree, effectively constructing a limit, while pushouts merge two objects along a common subobject to create a colimit that amalgamates structures. The key difference lies in their direction: equalizers solve the problem of "equalizing" morphisms via limits, whereas pushouts build new objects by "pushing out" along shared morphisms, emphasizing their duality in the categorical framework.
Applications of Equalizer in Mathematics
Equalizers in mathematics are fundamental in category theory and algebra, used to identify elements that map identically under two morphisms, enabling the construction of subobjects that represent solutions to equations. They play a critical role in defining limits, facilitating the study of algebraic structures, and providing a framework for comparing functors. This application of equalizers aids in solving problems related to kernels, pullbacks, and maintaining consistency across various mathematical structures.
Applications of Pushout in Mathematics
Pushouts play a crucial role in category theory, with diverse applications including constructing colimits, gluing spaces in topology, and defining fibered coproducts in algebraic structures. Pushouts enable the combination of objects along shared subobjects, facilitating the creation of new mathematical structures from existing ones. Their utility spans from defining universal properties in homological algebra to modeling pushout squares that describe the amalgamation of groups and modules.
Equalizer vs Pushout: Category Theory Perspective
Equalizer and pushout in category theory serve dual purposes: an equalizer identifies an object that universally equates two morphisms, while a pushout constructs an object that universally coalesces two morphisms sharing a common domain. The equalizer corresponds to a limit that picks out a subobject imposing equality constraints, often visualized in diagrammatic form with monomorphisms. Pushouts, as colimits, systematically combine objects via shared morphisms, crucial in constructions such as coequalizers, amalgamations, and fibered coproducts.
Visual Representation of Equalizer and Pushout
The visual representation of an equalizer typically involves two parallel morphisms with a universal object mapping into them, highlighting their point of equality within a category. In contrast, a pushout is depicted using a commutative square where two morphisms diverge from a common domain and converge into a universal object, emphasizing their joint coequalization. Diagrammatic clarity in category theory relies on these distinct shapes: the equalizer's forked structure versus the pushout's square, each encapsulating different universal properties.
Advantages and Limitations of Equalizer and Pushout
Equalizers provide precise identification of commonalities between morphisms, ensuring exact limits in category theory, but may be limited by complexity in large structures and computational overhead. Pushouts offer a constructive way to combine objects along shared substructures, enabling the creation of new objects from existing ones, yet they can lead to ambiguity or loss of information if the amalgamation is not well-defined. Both concepts are fundamental for understanding limits and colimits, with equalizers excelling in precise intersection scenarios and pushouts facilitating object amalgamation.
Conclusion: Choosing Between Equalizer and Pushout
Choosing between Equalizer and Pushout depends on the specific categorical or algebraic context and the properties desired in the resulting construction. Equalizers are ideal for capturing the largest subobject where two morphisms agree, often used to define limits and kernels in category theory. Pushouts serve to amalgamate objects along a shared subobject, crucial for colimits and gluing constructions in algebra, topology, and computer science.
Equalizer Infographic
 libterm.com
libterm.com