Field of sets is a collection of sets closed under finite unions, intersections, and complements, forming a fundamental structure in measure theory and probability. Understanding the properties of fields of sets helps you grasp how complex events and outcomes are constructed in mathematical frameworks. Explore the rest of the article to deepen your knowledge of fields of sets and their applications.
Table of Comparison
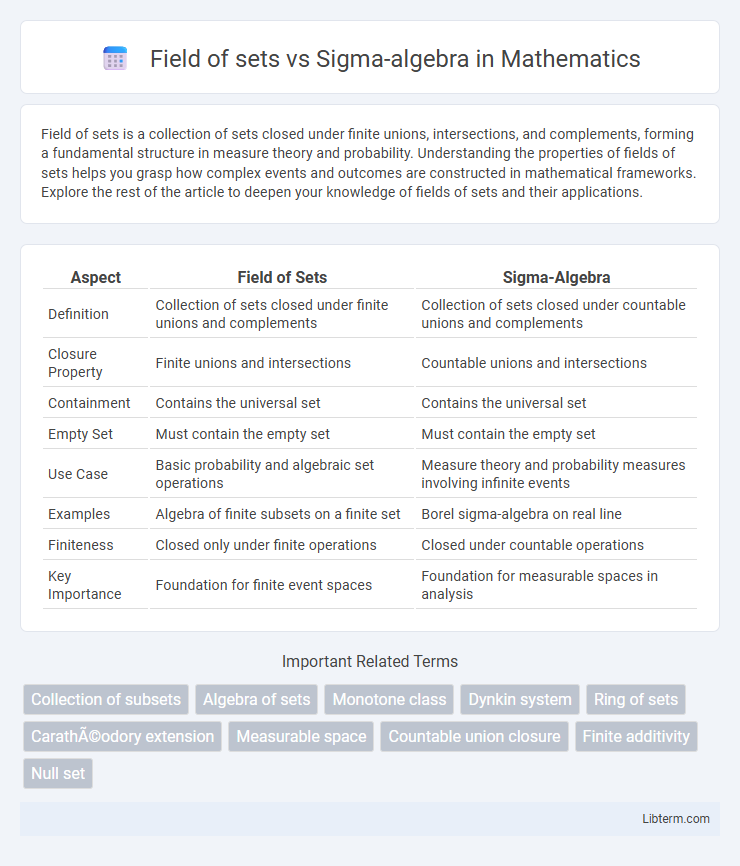
| Aspect | Field of Sets | Sigma-Algebra |
|---|---|---|
| Definition | Collection of sets closed under finite unions and complements | Collection of sets closed under countable unions and complements |
| Closure Property | Finite unions and intersections | Countable unions and intersections |
| Containment | Contains the universal set | Contains the universal set |
| Empty Set | Must contain the empty set | Must contain the empty set |
| Use Case | Basic probability and algebraic set operations | Measure theory and probability measures involving infinite events |
| Examples | Algebra of finite subsets on a finite set | Borel sigma-algebra on real line |
| Finiteness | Closed only under finite operations | Closed under countable operations |
| Key Importance | Foundation for finite event spaces | Foundation for measurable spaces in analysis |
Introduction to Set Theory in Measure Spaces
A field of sets is a collection closed under finite unions and complementation, forming the basis for constructing measurable spaces in set theory. In contrast, a sigma-algebra extends these properties by allowing countable unions, essential for defining measures that accommodate infinite operations. Understanding the distinction between fields and sigma-algebras is fundamental in measure spaces, as sigma-algebras enable rigorous integration and probability theory frameworks.
Defining a Field of Sets
A field of sets is a non-empty collection of subsets of a given set that is closed under finite unions, finite intersections, and complements relative to the original set. Every finite union or intersection of sets in a field also belongs to the field, ensuring algebraic operations remain internal. Unlike sigma-algebras, fields of sets do not require closure under countable unions, making them a less restrictive structure in measure theory and set algebra.
What is a Sigma-Algebra?
A Sigma-algebra is a collection of subsets of a given set that is closed under countable unions, countable intersections, and complements relative to the original set, making it fundamental in measure theory. Unlike a field of sets, which is only closed under finite unions and intersections, a Sigma-algebra supports infinite operations essential for defining measures and integration on spaces. This structure enables rigorous mathematical frameworks for probability, enabling the assignment of consistent probabilities to potentially infinite collections of events.
Key Differences: Field of Sets vs Sigma-Algebra
A field of sets is a collection of subsets closed under finite unions, finite intersections, and complements, whereas a sigma-algebra extends this closure to countable unions and countable intersections. Sigma-algebras guarantee closure under limits of sequences of sets, making them essential in measure theory and probability for defining measures on infinite spaces. Fields of sets are generally simpler structures useful in finite or discrete contexts, while sigma-algebras support advanced integration and limit operations in more complex spaces.
Closure Properties: Comparison and Contrast
Fields of sets are closed under finite union and intersection, as well as complement relative to the universal set, whereas sigma-algebras extend this closure to countable unions and intersections. In contrast to fields, sigma-algebras guarantee closure under countable operations, which is essential for defining measures and integrating functions over infinite collections. This fundamental difference in closure properties distinguishes sigma-algebras as a more robust structure in measure theory compared to fields of sets.
Examples Illustrating Fields and Sigma-Algebras
Fields of sets include collections like finite unions of intervals on the real line, demonstrating closure under finite unions and complements, such as the algebra generated by all half-open intervals [a, b). Sigma-algebras extend this concept by allowing countable unions and intersections, exemplified by the Borel sigma-algebra containing all open sets and their countable unions in a topological space. These examples highlight that all sigma-algebras are fields of sets, but fields are not necessarily sigma-algebras without closure under countable operations.
Importance in Probability and Measure Theory
Fields of sets provide a basic structure closed under finite unions and complements, essential for constructing preliminary collections of events in probability. Sigma-algebras extend this concept by requiring closure under countable unions, forming the foundation for defining measures and enabling the rigorous development of probability spaces. The distinction is crucial for measure theory because sigma-algebras allow the handling of infinite event collections, ensuring well-defined probability measures on complex sample spaces.
When to Use a Field of Sets vs a Sigma-Algebra
A field of sets is suitable for finite or simpler measure spaces where closure under finite unions and complements suffices, often applied in probability with finite sample spaces. A sigma-algebra is necessary in contexts requiring countable operations, such as defining Lebesgue measure or studying stochastic processes, due to its closure under countable unions and complements. Choosing between a field of sets and a sigma-algebra depends on whether countable additivity and limits of infinite sequences of sets are essential in the analysis.
Real-World Applications and Implications
Field of sets and sigma-algebras serve as foundational structures in measure theory, with sigma-algebras being crucial for defining probability measures used in statistical modeling and machine learning. Fields of sets, though algebraically simpler due to closure under finite operations, are often inadequate for handling infinite or countable processes essential in real-world applications like financial risk assessment and quantum physics. Sigma-algebras provide the necessary framework for managing infinite data and ensuring measurable sets, enabling robust and consistent analysis in diverse domains such as epidemiology and signal processing.
Summary and Further Reading
A field of sets is a collection closed under finite unions and complements, while a sigma-algebra extends this closure to countable unions, essential for measure theory. Sigma-algebras support the construction of measures and integration, making them foundational in probability and analysis. For deeper understanding, consult "Measure Theory" by Paul Halmos and "Real Analysis" by H.L. Royden.
Field of sets Infographic
 libterm.com
libterm.com