A discrete group is a mathematical concept where the group elements form a set with the discrete topology, meaning each element is isolated from others without any accumulation points. These groups often appear in geometry, algebra, and number theory, playing a crucial role in understanding symmetries and structures. Explore the rest of the article to deepen your grasp of discrete groups and their applications.
Table of Comparison
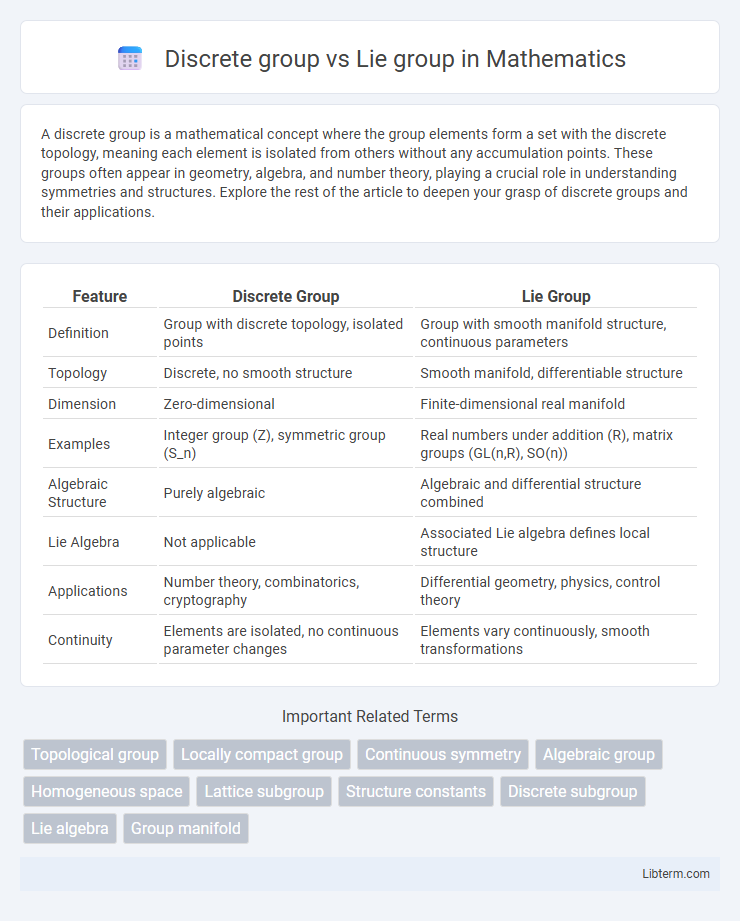
| Feature | Discrete Group | Lie Group |
|---|---|---|
| Definition | Group with discrete topology, isolated points | Group with smooth manifold structure, continuous parameters |
| Topology | Discrete, no smooth structure | Smooth manifold, differentiable structure |
| Dimension | Zero-dimensional | Finite-dimensional real manifold |
| Examples | Integer group (Z), symmetric group (S_n) | Real numbers under addition (R), matrix groups (GL(n,R), SO(n)) |
| Algebraic Structure | Purely algebraic | Algebraic and differential structure combined |
| Lie Algebra | Not applicable | Associated Lie algebra defines local structure |
| Applications | Number theory, combinatorics, cryptography | Differential geometry, physics, control theory |
| Continuity | Elements are isolated, no continuous parameter changes | Elements vary continuously, smooth transformations |
Introduction to Discrete Groups and Lie Groups
Discrete groups consist of isolated points with no continuous parameters, often studied through their algebraic properties and symmetries in finite or countable sets. Lie groups are smooth manifolds equipped with both group and differentiable structure, allowing for continuous symmetries represented by differential equations. Understanding the fundamental differences between discrete and Lie groups is crucial in fields such as geometry, algebra, and mathematical physics.
Fundamental Definitions and Key Concepts
A discrete group is a group equipped with the discrete topology, where every element forms an open set, emphasizing purely algebraic structure without continuous parameters. In contrast, a Lie group is a smooth manifold with a group structure allowing continuous and differentiable operations, blending algebraic and geometric properties. Lie groups serve as the foundation for studying continuous symmetries and have associated Lie algebras capturing infinitesimal structure absent in discrete groups.
Algebraic Structure: Discrete vs. Continuous
Discrete groups consist of isolated elements with purely algebraic structures characterized by countable operations, while Lie groups possess a continuous manifold structure allowing smooth operations and differentiable group actions. The algebraic structure of discrete groups emphasizes combinatorial and topological rigidity, contrasting with Lie groups' reliance on continuous symmetries described through Lie algebras. Understanding these differences enables applications ranging from symmetry analysis in crystallography to continuous transformation groups in physics.
Topological Properties and Their Implications
Discrete groups exhibit a topology where each singleton set is open, making them totally disconnected with no limit points, which results in simpler topological structures but limits continuous symmetries. Lie groups, as smooth manifolds, possess rich topological properties including connectedness, compactness, and differentiability, enabling continuous group actions and deep geometric interpretations. These topological distinctions influence applications, with discrete groups prominent in algebraic and combinatorial contexts, while Lie groups underpin continuous symmetries in physics and differential geometry.
Examples of Discrete Groups in Mathematics
Examples of discrete groups in mathematics include the group of integers under addition (Z), finite groups such as the symmetric group S_n, and Fuchsian groups acting on the hyperbolic plane. These groups are characterized by isolated points with no continuous parameters, contrasting Lie groups like SO(3) or SU(2) that form smooth manifolds with continuous symmetries. Discrete groups often appear in number theory, topology, and geometry, playing crucial roles in tessellations, crystallography, and the study of fundamental groups.
Common Lie Groups and Their Roles
Common Lie groups such as SO(n), SU(n), and GL(n) play crucial roles in mathematics and physics by providing continuous symmetry structures characterized by smooth manifolds and group operations. Discrete groups, lacking this smooth structure, serve primarily in algebraic and combinatorial contexts, while Lie groups enable the study of differential equations, particle physics, and geometry through their continuous transformations. The interplay between discrete subgroups and Lie groups, as seen in crystallography and quantum mechanics, highlights their complementary applications in symmetry and group theory.
Group Actions: Discrete vs. Lie Groups
Discrete groups act on spaces through isolated transformations, which produce orbit structures with distinct, separated points, often leading to combinatorial or topological applications. Lie groups, equipped with smooth manifold structures, enable continuous group actions that form differentiable orbits and facilitate symmetry analysis in geometry and physics. The continuous nature of Lie group actions allows for the use of calculus and differential geometry, contrasting the purely algebraic or topological methods employed in discrete group actions.
Applications in Geometry and Physics
Discrete groups play a crucial role in geometry by classifying symmetrical structures such as crystal lattices and tessellations, whereas Lie groups provide a continuous framework essential for analyzing smooth symmetries in differentiable manifolds. In physics, Lie groups underpin fundamental theories like gauge theory and general relativity through their representation of continuous symmetries of spacetime and internal particle states. Discrete groups also appear in quantum physics, particularly in the study of finite symmetry groups relevant to particle physics and condensed matter systems.
Connections and Differences in Representation Theory
Discrete groups have representations characterized by finite or countable sets, often realized as permutation or matrix groups over discrete fields, while Lie groups involve continuous symmetries represented by smooth homomorphisms into matrix groups over real or complex fields. The representation theory of Lie groups heavily relies on differential geometry and Lie algebras, enabling the classification of irreducible representations via highest weight theory and the use of continuous parameters. Discrete groups lack this differential structure, making their representation theory more combinatorial and algebraic, with an emphasis on character theory and group cohomology rather than analytic methods.
Summary: Discrete Groups vs. Lie Groups Comparison
Discrete groups consist of isolated elements with no continuous structure, often represented by finite or countable sets with group operations. Lie groups combine group theory with smooth manifold structure, enabling continuous transformations and differentiable symmetries characterized by Lie algebras. The fundamental difference lies in topology and smoothness: discrete groups lack a differentiable structure, whereas Lie groups support continuous symmetries and have applications in physics and geometry.
Discrete group Infographic
 libterm.com
libterm.com