A preadditive category is a category enriched over the category of abelian groups, meaning that each hom-set is equipped with an abelian group structure and composition of morphisms is bilinear. This structure provides a natural framework for studying additive properties in algebra and category theory, allowing you to work with morphisms that can be added and scaled. Explore the rest of the article to understand the foundational role of preadditive categories in advanced mathematical contexts.
Table of Comparison
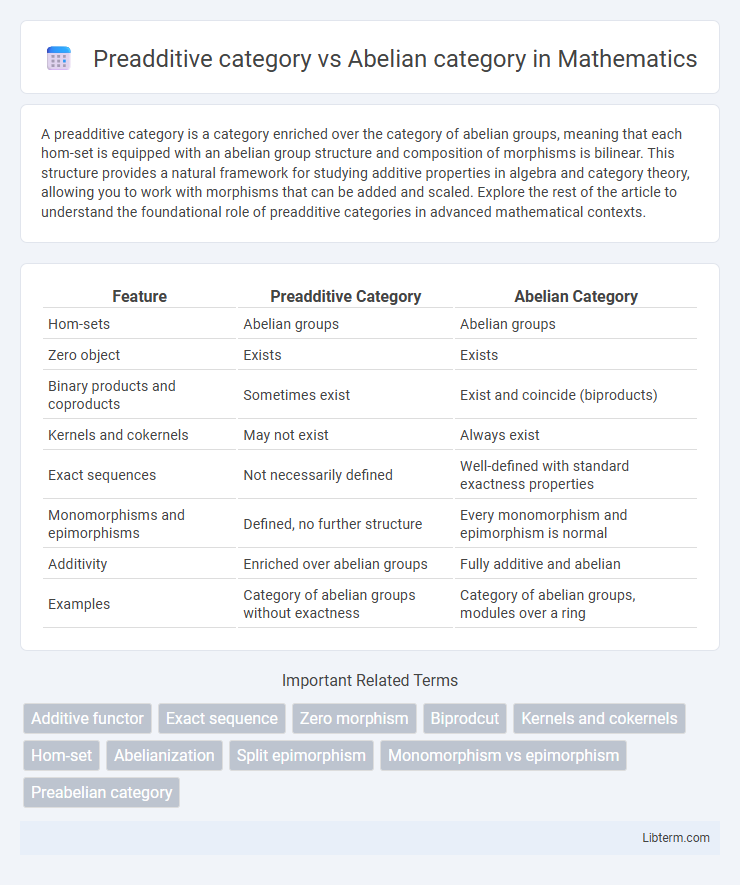
| Feature | Preadditive Category | Abelian Category |
|---|---|---|
| Hom-sets | Abelian groups | Abelian groups |
| Zero object | Exists | Exists |
| Binary products and coproducts | Sometimes exist | Exist and coincide (biproducts) |
| Kernels and cokernels | May not exist | Always exist |
| Exact sequences | Not necessarily defined | Well-defined with standard exactness properties |
| Monomorphisms and epimorphisms | Defined, no further structure | Every monomorphism and epimorphism is normal |
| Additivity | Enriched over abelian groups | Fully additive and abelian |
| Examples | Category of abelian groups without exactness | Category of abelian groups, modules over a ring |
Introduction to Category Theory
Preadditive categories are enriched over the category of abelian groups, meaning each hom-set is an abelian group and composition of morphisms is bilinear, providing a natural framework for additive structures in category theory. Abelian categories extend preadditive categories by requiring all morphisms to have kernels and cokernels, and ensuring every monomorphism and epimorphism is normal, facilitating exact sequences and homological algebra. Understanding the distinctions between preadditive and Abelian categories is fundamental in category theory for studying modules, sheaves, and derived functors in abstract algebra and algebraic geometry.
Defining Preadditive Categories
Preadditive categories are categories enriched over the category of abelian groups, meaning each hom-set forms an abelian group and composition is bilinear. This structure generalizes the additive nature of morphisms without requiring kernels or cokernels, which are essential in abelian categories. Unlike abelian categories, preadditive categories do not necessarily have all finite limits or colimits, but their hom-sets allow direct addition of morphisms reflecting the additive algebraic structure.
Key Properties of Preadditive Categories
Preadditive categories are enriched over the category of abelian groups, meaning their hom-sets carry an abelian group structure compatible with composition, allowing morphism addition and zero morphisms. Unlike Abelian categories, which require all kernels and cokernels and exactness properties, preadditive categories only guarantee additive structure without necessitating limits or quotients. Key properties include bilinearity of composition and the existence of a zero morphism for every pair of objects, making them foundational for additive category theory and homological algebra.
Exploring Abelian Categories
Abelian categories generalize preadditive categories by incorporating kernels and cokernels that satisfy exactness conditions, enabling a robust framework for homological algebra. Unlike preadditive categories, which only require hom-sets to be abelian groups and composition to be bilinear, abelian categories demand that every morphism has a kernel and cokernel, and that all monomorphisms and epimorphisms are normal. This structure allows abelian categories to support exact sequences, providing a powerful foundation for algebraic topology, representation theory, and homological algebra.
Fundamental Differences Between Preadditive and Abelian Categories
Preadditive categories have hom-sets that are abelian groups with bilinear composition, enabling addition of morphisms but lacking kernels or cokernels required for exact sequences. Abelian categories extend preadditive structure by enforcing that every morphism admits a kernel and cokernel, ensuring all monomorphisms and epimorphisms are normal. This fundamental difference enables abelian categories to support homological algebra, unlike the more general preadditive categories.
Morphisms in Preadditive and Abelian Contexts
Morphisms in preadditive categories form abelian groups, enabling addition and zero morphisms between any two objects, which structures the hom-sets with additive operations. In abelian categories, morphisms not only have additive structures but also possess kernels and cokernels, facilitating exact sequences and homological algebra. The enhanced morphism structure in abelian categories supports stronger categorical properties such as exactness, images, and coimages, distinguishing them from merely preadditive contexts.
Exact Sequences and Homological Aspects
Preadditive categories are enriched over abelian groups, allowing morphism sets to carry an additive structure essential for defining kernels and cokernels, but they do not necessarily guarantee exactness properties needed for homological algebra. Abelian categories extend preadditive categories by requiring all morphisms to have kernels and cokernels, ensuring that every monomorphism and epimorphism is normal, which enables the construction of exact sequences fundamental in homological analysis. Exact sequences in abelian categories provide a robust framework for defining derived functors, Ext and Tor groups, and facilitate homological dimension theory, making abelian categories a crucial setting for advanced homological methods.
Examples of Preadditive and Abelian Categories
Preadditive categories include examples such as the category of abelian groups, where hom-sets are endowed with abelian group structures, and the category of modules over a ring, which extends additive hom-sets with module actions. Abelian categories are exemplified by categories like the category of abelian groups, categories of modules over a ring, and the category of coherent sheaves on a scheme, all possessing kernels, cokernels, and exact sequences facilitating homological algebra. While every abelian category is preadditive, the converse does not hold as preadditive categories lack the full structural properties such as exactness required to be abelian.
Applications in Algebra and Topology
Preadditive categories, characterized by hom-sets forming abelian groups, facilitate the formalization of linear algebraic structures fundamental in module theory and representation theory, enabling the study of morphisms with additive properties. Abelian categories extend this framework by incorporating kernels and cokernels, allowing exact sequences crucial for homological algebra applications such as computing derived functors and spectral sequences. In topology, abelian categories underpin the construction of chain complexes and homology theories, providing a robust categorical context for persistent homology and sheaf cohomology.
Conclusion: Choosing Between Preadditive and Abelian Categories
Preadditive categories provide a framework where hom-sets are equipped with abelian group structures, enabling additive operations but without requiring kernels or cokernels. Abelian categories extend preadditive categories by ensuring the existence of all kernels, cokernels, and exact sequences, making them ideal for homological algebra and more robust structural analysis. Selecting between preadditive and abelian categories depends on whether the mathematical context demands full exactness properties and rich homological tools (abelian) or simply additive structure without exactness requirements (preadditive).
Preadditive category Infographic
 libterm.com
libterm.com