A bounded operator is a linear transformation between normed vector spaces that maps bounded sets to bounded sets, ensuring the operator's norm is finite. This property guarantees stability and continuity, crucial for analyzing functional analysis problems and operator theory. Discover how bounded operators influence various mathematical frameworks and their practical applications in the full article.
Table of Comparison
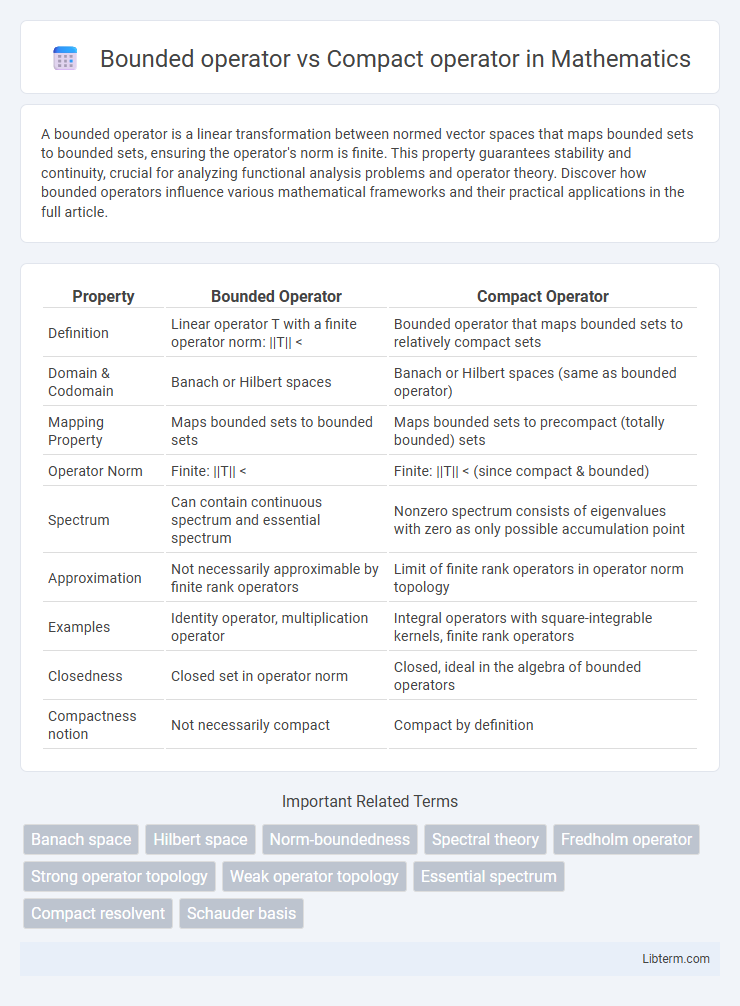
| Property | Bounded Operator | Compact Operator |
|---|---|---|
| Definition | Linear operator T with a finite operator norm: ||T|| < | Bounded operator that maps bounded sets to relatively compact sets |
| Domain & Codomain | Banach or Hilbert spaces | Banach or Hilbert spaces (same as bounded operator) |
| Mapping Property | Maps bounded sets to bounded sets | Maps bounded sets to precompact (totally bounded) sets |
| Operator Norm | Finite: ||T|| < | Finite: ||T|| < (since compact & bounded) |
| Spectrum | Can contain continuous spectrum and essential spectrum | Nonzero spectrum consists of eigenvalues with zero as only possible accumulation point |
| Approximation | Not necessarily approximable by finite rank operators | Limit of finite rank operators in operator norm topology |
| Examples | Identity operator, multiplication operator | Integral operators with square-integrable kernels, finite rank operators |
| Closedness | Closed set in operator norm | Closed, ideal in the algebra of bounded operators |
| Compactness notion | Not necessarily compact | Compact by definition |
Introduction to Bounded and Compact Operators
Bounded operators are linear transformations between normed vector spaces that map bounded sets to bounded sets, ensuring continuity and stability in functional analysis. Compact operators are a special subset of bounded operators characterized by mapping bounded sets to relatively compact sets, often leading to approximations by finite-rank operators. The distinction between bounded and compact operators is fundamental in operator theory, affecting spectral properties and applications in solving integral equations.
Definitions: Bounded vs Compact Operators
A bounded operator is a linear operator between normed vector spaces that maps bounded sets to bounded sets, ensuring continuity and the existence of a finite operator norm. A compact operator is a bounded linear operator that maps bounded sets into relatively compact sets, meaning the image has compact closure, often implying the operator can be approximated by finite-rank operators. While every compact operator is bounded, not all bounded operators are compact, distinguishing their structural and spectral properties in functional analysis.
Key Properties of Bounded Operators
Bounded operators are linear operators between normed vector spaces that map bounded sets to bounded sets, ensuring continuity and stability in functional analysis. Key properties include the existence of a finite operator norm, linearity, and the preservation of limits for convergent sequences. Unlike compact operators, bounded operators may not necessarily compress infinite-dimensional subsets into relatively compact ones, highlighting their broader applicability.
Essential Features of Compact Operators
Compact operators on Banach spaces map bounded sets to relatively compact sets, meaning their image has compact closure, unlike general bounded operators which only guarantee boundedness. Essential features of compact operators include the approximation property by finite-rank operators and the fact that their spectrum, except possibly zero, consists of eigenvalues of finite multiplicity. These characteristics make compact operators crucial in Fredholm theory and spectral analysis, distinguishing them from merely bounded operators.
Differences in Operator Behavior
Bounded operators map bounded sets to bounded sets, ensuring stability and continuity in infinite-dimensional spaces, while compact operators map bounded sets to relatively compact sets, resulting in images with limit points and often exhibiting finite-rank approximations. Compact operators can be seen as a stronger condition, implying boundedness but also enabling spectral properties similar to matrices, such as having eigenvalues accumulating only at zero. The key behavioral difference lies in compact operators' ability to approximate infinite-dimensional problems with finite-dimensional analogs, which bounded operators in general do not guarantee.
Examples of Bounded Operators
Bounded operators, such as the identity operator and multiplication by a fixed scalar on a Hilbert space, maintain continuity and map bounded sets to bounded sets, ensuring stability in functional analysis. For example, the differentiation operator defined on the space of continuously differentiable functions is bounded when restricted to certain subspaces. In contrast, compact operators, like the integral operator with a square-integrable kernel, map bounded sets to relatively compact sets and often arise in solving integral equations.
Examples of Compact Operators
Compact operators on infinite-dimensional Hilbert spaces often appear as integral operators with square-integrable kernels, such as the Volterra operator defined by \((Tf)(x) = \int_0^x f(t) dt\). Finite-rank operators, which map the entire space into a finite-dimensional subspace, serve as basic examples of compact operators, including projections onto finite-dimensional subspaces. Unlike bounded operators that may lack compactness, these compact operators are limit points of finite-rank operators in the operator norm topology, playing a crucial role in spectral theory and functional analysis.
Relationships Between Boundedness and Compactness
Bounded operators on normed spaces are linear maps that map bounded sets to bounded sets, ensuring continuity, while compact operators are a subset of bounded operators that map bounded sets to relatively compact sets, meaning their images have compact closure. Every compact operator is bounded, but the converse is not true; bounded operators need not have compact images. The relationship highlights that compactness imposes a stronger condition than boundedness, involving the operator's ability to approximate sequences by finite-dimensional maps.
Applications in Functional Analysis
Bounded operators play a crucial role in functional analysis by ensuring stability and continuity of linear transformations between normed spaces, which is essential for solving differential equations and studying Banach spaces. Compact operators extend these concepts by approximating infinite-dimensional problems with finite-rank operators, facilitating spectral theory applications such as the analysis of eigenvalues and Fredholm theory. Functional analysis leverages bounded and compact operators to develop effective methods in optimization, partial differential equations, and integral equations, enhancing both theoretical insights and practical computations.
Summary and Comparative Insights
Bounded operators on normed spaces map bounded sets to bounded sets and are continuous linear transformations, while compact operators not only are bounded but also map bounded sets to relatively compact sets with compact closure. Every compact operator is bounded, but the converse is generally false; compactness implies stronger structural properties facilitating spectral analysis and approximation by finite-rank operators. The distinctions influence functional analysis applications, where boundedness ensures continuity and compactness yields compact spectral characteristics and enhanced operator behavior in infinite-dimensional spaces.
Bounded operator Infographic
 libterm.com
libterm.com