A local maximum is a point in a function where the value is higher than all nearby points within a certain interval, though not necessarily the highest overall value. Identifying local maxima is crucial for understanding the behavior of functions in calculus, optimization, and data analysis. Explore the rest of the article to learn how to find and apply local maximum concepts effectively in various mathematical contexts.
Table of Comparison
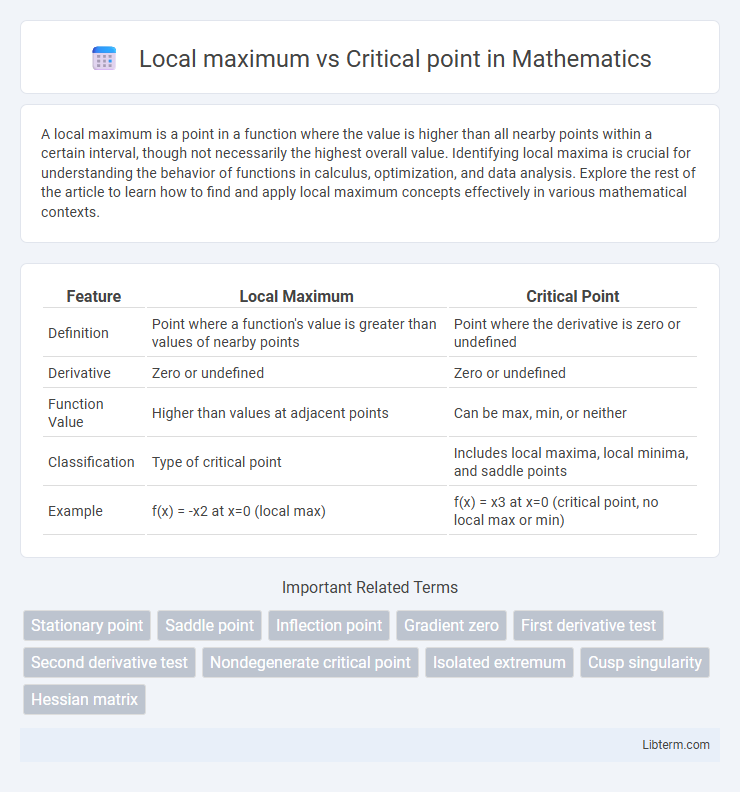
| Feature | Local Maximum | Critical Point |
|---|---|---|
| Definition | Point where a function's value is greater than values of nearby points | Point where the derivative is zero or undefined |
| Derivative | Zero or undefined | Zero or undefined |
| Function Value | Higher than values at adjacent points | Can be max, min, or neither |
| Classification | Type of critical point | Includes local maxima, local minima, and saddle points |
| Example | f(x) = -x2 at x=0 (local max) | f(x) = x3 at x=0 (critical point, no local max or min) |
Definition of Local Maximum
A local maximum is a point within a neighborhood where a function's value is greater than or equal to the values at all nearby points. It represents a peak in the function's graph, distinguishing it from other critical points such as minima or saddle points. Local maxima are critical points where the first derivative is zero or undefined, but not all critical points correspond to local maxima.
Understanding Critical Points
Critical points occur where the first derivative of a function equals zero or is undefined, indicating potential local maxima, minima, or saddle points. Local maxima represent critical points where the function values are higher than in their immediate vicinity, typically identified by a negative second derivative. Distinguishing critical points requires analyzing both the first and second derivatives to understand the nature of the function's behavior at those points.
Mathematical Criteria for Local Maximum
A local maximum occurs at a point where the first derivative of a function equals zero and the second derivative is negative, indicating concavity downwards. Critical points include locations where the first derivative is zero or undefined, encompassing local maxima, minima, and saddle points. The second derivative test serves as a key mathematical criterion to distinguish local maxima from other critical points by confirming the function's curvature.
Identifying Critical Points in Functions
Critical points of a function occur where its first derivative is zero or undefined, indicating potential local maxima, minima, or saddle points. Identifying critical points involves solving f'(x) = 0 and analyzing points where f'(x) does not exist, which helps locate key values for function behavior. These points are essential in calculus and optimization for determining where the function's slope changes and potential local extrema occur.
Differences Between Local Maximum and Critical Point
A local maximum is a point on a function where the value is greater than the values of neighboring points within a specific interval, representing a peak in the graph. A critical point occurs where the derivative of the function is zero or undefined, indicating potential local maxima, minima, or saddle points. The key difference is that while all local maxima are critical points, not all critical points correspond to local maxima, as some critical points represent minima or points of inflection.
Role of Derivatives in Finding Local Maxima and Critical Points
Derivatives play a crucial role in identifying local maxima and critical points by indicating where a function's slope is zero or undefined. A critical point occurs at values of x where the first derivative f'(x) equals zero or does not exist, signaling potential local maxima, minima, or saddle points. By applying the first and second derivative tests, mathematicians determine the nature of these critical points and confirm the presence of local maxima.
Graphical Interpretation of Local Maximum vs Critical Point
A local maximum on a graph is a point where the function value is higher than all nearby points, creating a peak in the curve, whereas a critical point is any point where the derivative is zero or undefined, including local maxima, minima, and saddle points. Graphically, local maxima appear as distinct peaks, while critical points encompass these along with flat inflection points where the slope changes sign but does not produce a peak or valley. Identifying local maxima involves examining critical points and analyzing the curvature or sign changes of the derivative around these points.
Real-World Examples Illustrating Both Concepts
Local maxima occur in various fields such as economics, where a business's profit curve peaks at a certain production level before declining. Critical points, including local maxima, minima, and saddle points, are crucial in engineering, for instance, when optimizing stress distribution in structural design to prevent material failure. In finance, identifying critical points on price charts helps traders forecast potential reversals or breakouts, illustrating the practical importance of these mathematical concepts.
Common Misconceptions Between Local Maximum and Critical Point
Local maximum and critical point are often confused, but they represent different mathematical concepts. A critical point occurs where the derivative of a function is zero or undefined and can correspond to a local maximum, local minimum, or neither, such as a saddle point. Misconceptions arise when assuming every critical point is a local maximum, ignoring points that are local minima or points of inflection.
Importance in Calculus and Optimization Problems
Local maxima indicate points where a function attains higher values than nearby points, essential for identifying optimal solutions in optimization problems. Critical points, where the derivative is zero or undefined, serve as candidates for local maxima, minima, or saddle points, making their analysis crucial in calculus for understanding function behavior. Distinguishing between local maxima and other critical points ensures accurate determination of optimal values in real-world optimization scenarios.
Local maximum Infographic
 libterm.com
libterm.com