Zariski's Lemma is a fundamental result in commutative algebra stating that if a finitely generated algebra over a field is a field itself, then it is a finite extension of that field. This lemma plays a crucial role in algebraic geometry and ring theory by establishing the algebraic closure properties of certain field extensions. Explore the rest of the article to understand how Zariski's Lemma influences modern mathematical theories and applications.
Table of Comparison
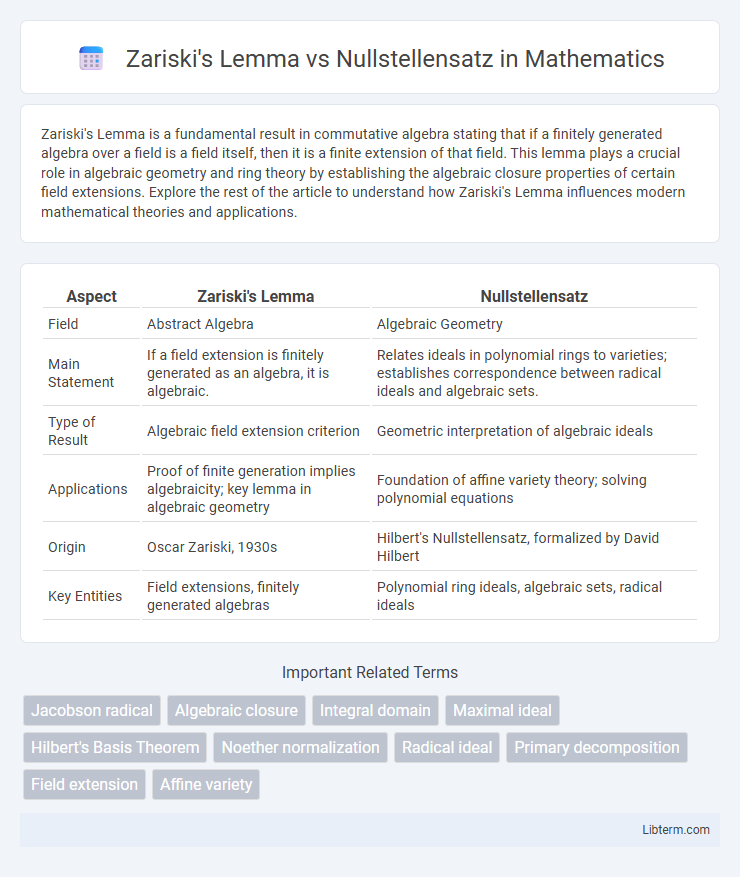
| Aspect | Zariski's Lemma | Nullstellensatz |
|---|---|---|
| Field | Abstract Algebra | Algebraic Geometry |
| Main Statement | If a field extension is finitely generated as an algebra, it is algebraic. | Relates ideals in polynomial rings to varieties; establishes correspondence between radical ideals and algebraic sets. |
| Type of Result | Algebraic field extension criterion | Geometric interpretation of algebraic ideals |
| Applications | Proof of finite generation implies algebraicity; key lemma in algebraic geometry | Foundation of affine variety theory; solving polynomial equations |
| Origin | Oscar Zariski, 1930s | Hilbert's Nullstellensatz, formalized by David Hilbert |
| Key Entities | Field extensions, finitely generated algebras | Polynomial ring ideals, algebraic sets, radical ideals |
Introduction to Zariski's Lemma and Nullstellensatz
Zariski's Lemma states that any finitely generated algebra over a field that is also a field must be a finite field extension, highlighting the algebraic nature of field extensions in commutative algebra. The Nullstellensatz, a fundamental theorem in algebraic geometry, establishes a correspondence between ideals in polynomial rings over algebraically closed fields and algebraic sets, providing a geometric interpretation of algebraic properties. Both results form the backbone of algebraic geometry by linking algebraic structures and geometric intuition, with Zariski's Lemma underpinning the proof of the Nullstellensatz.
Historical Context and Motivation
Zariski's Lemma, formulated by Oscar Zariski in the 1930s, addresses the algebraic closure properties of fields in the context of commutative algebra, serving as a crucial tool in proving Hilbert's Nullstellensatz. The Nullstellensatz, established by David Hilbert in 1890, provided a foundational link between algebraic geometry and polynomial ideals, catalyzing the study of solution sets of polynomial equations over algebraically closed fields. Both results emerged from the effort to understand polynomial equations' structure, with Zariski's Lemma refining the algebraic framework that underpins the Nullstellensatz's geometric interpretations.
Statement of Zariski's Lemma
Zariski's Lemma states that if a field extension \( L/K \) is finitely generated as a \( K \)-algebra and \( L \) is a field, then \( L \) is a finite algebraic extension of \( K \). This lemma serves as a key step in proving the Hilbert Nullstellensatz, which relates algebraic sets over an algebraically closed field to radical ideals in polynomial rings. The lemma's statement emphasizes the finite generation and field structure, distinguishing it from the Nullstellensatz's broader geometric interpretations.
The Nullstellensatz: Statement and Variants
The Nullstellensatz, a cornerstone in algebraic geometry, establishes a fundamental correspondence between ideals in polynomial rings and algebraic sets over an algebraically closed field. Its classical form, Hilbert's Nullstellensatz, states that if a polynomial vanishes on the common zeroes of an ideal, then some power of the polynomial lies in that ideal, connecting algebraic geometry to ideal theory. Variants like the Weak and Strong Nullstellensatz refine this relationship by characterizing maximal ideals and radical ideals, with profound implications for solving polynomial equations and the structure of affine varieties.
Algebraic Foundations: Fields, Ideals, and Rings
Zariski's Lemma states that if a finitely generated algebra over a field is also a field, then it is a finite field extension of the base field, emphasizing the role of field extensions in algebraic geometry. Hilbert's Nullstellensatz connects ideals in polynomial rings over algebraically closed fields with algebraic sets, revealing a duality between radical ideals and varieties, hence foundational in understanding the correspondence between algebraic structures and geometric objects. Both results underpin the study of algebraic varieties by relating properties of fields, ideals, and rings, with Zariski's Lemma ensuring finite generation leads to field extensions and Nullstellensatz providing a bridge between ideal theory and geometry.
Relationship Between Zariski's Lemma and Nullstellensatz
Zariski's Lemma serves as a foundational algebraic tool that directly supports the proof of the Weak Nullstellensatz by establishing that a finitely generated algebra over a field that is also a field is a finite field extension. This lemma links the algebraic structure of polynomial rings with their maximal ideals, facilitating the characterization of solutions to polynomial equations in algebraically closed fields provided by the Nullstellensatz. The hierarchical relationship shows Zariski's Lemma as a key step in the algebraic reasoning that underpins the Nullstellensatz's geometric interpretation of polynomial ideals and zero sets.
Proof Sketches and Key Insights
Zariski's Lemma establishes that a finitely generated algebra over a field, which is also a field, must be a finite extension of the base field, relying on the construction of a transcendence basis and induction on the number of generators. The Hilbert Nullstellensatz connects algebraic sets with ideals in polynomial rings, demonstrated through the use of maximal ideals and the correspondence between points and evaluation homomorphisms. Key insights highlight that Zariski's Lemma serves as a foundational step in proving the Nullstellensatz by linking algebraic field extensions to geometric points in affine space.
Applications in Algebraic Geometry
Zariski's Lemma is pivotal in algebraic geometry for proving that finitely generated algebras over fields are fields, aiding the study of algebraic varieties' coordinate rings. The Nullstellensatz provides a fundamental correspondence between ideals in polynomial rings and algebraic sets, enabling the translation of geometric properties into algebraic conditions. Both theorems underpin the duality between algebraic varieties and their coordinate rings, facilitating the resolution of geometric problems via algebraic methods.
Differences and Distinctions in Usage
Zariski's Lemma primarily provides a crucial algebraic tool by asserting that a finitely generated algebra over a field, which is also a field, must be a finite extension of that field, useful in field theory and algebraic geometry. In contrast, Hilbert's Nullstellensatz establishes a profound correspondence between ideals in polynomial rings and algebraic sets, forming a foundational result for algebraic geometry by linking algebraic varieties with their defining ideals. While Zariski's Lemma simplifies understanding field extensions in finitely generated algebras, Nullstellensatz is instrumental in encoding geometric properties into algebraic structures, highlighting their complementary roles in commutative algebra and geometry.
Conclusion and Further Reading
Zariski's Lemma establishes that a finitely generated algebra over a field that is also a field must be a finite extension of the base field, serving as a fundamental step in proving the Nullstellensatz. The Nullstellensatz concludes that maximal ideals in polynomial rings over algebraically closed fields correspond precisely to points in affine space, linking algebraic geometry with commutative algebra. For further reading, explore algebraic geometry textbooks like Hartshorne's "Algebraic Geometry" and Eisermann's "Algebraic Foundations," which provide in-depth proofs and applications of both theorems.
Zariski's Lemma Infographic
 libterm.com
libterm.com