Diagonal lines in design create dynamic movement and visual interest by guiding the viewer's eye across a composition. Their angular orientation adds energy and can make layouts feel more engaging and less static. Discover how incorporating diagonals can transform your creative projects by reading the rest of this article.
Table of Comparison
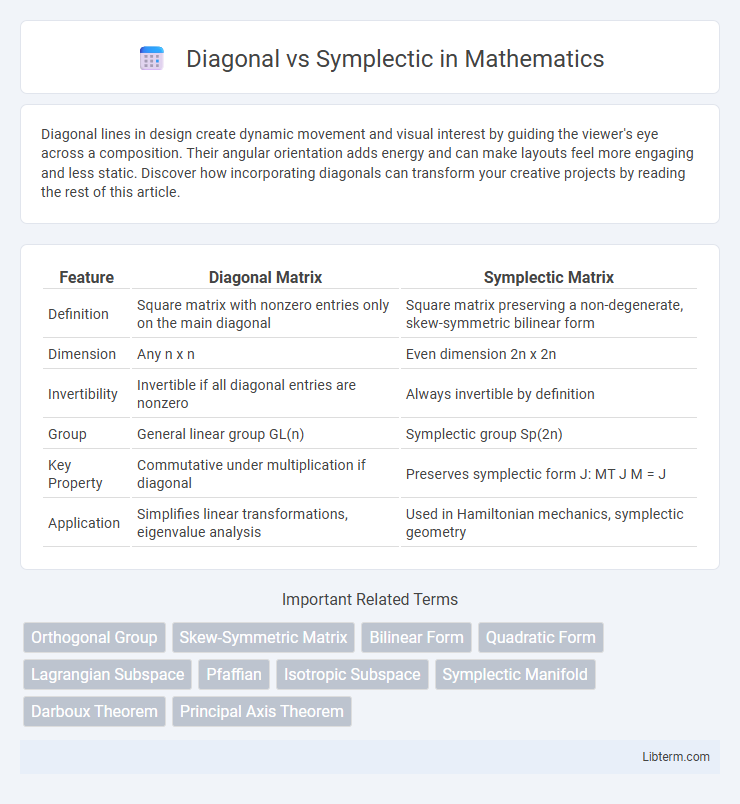
| Feature | Diagonal Matrix | Symplectic Matrix |
|---|---|---|
| Definition | Square matrix with nonzero entries only on the main diagonal | Square matrix preserving a non-degenerate, skew-symmetric bilinear form |
| Dimension | Any n x n | Even dimension 2n x 2n |
| Invertibility | Invertible if all diagonal entries are nonzero | Always invertible by definition |
| Group | General linear group GL(n) | Symplectic group Sp(2n) |
| Key Property | Commutative under multiplication if diagonal | Preserves symplectic form J: MT J M = J |
| Application | Simplifies linear transformations, eigenvalue analysis | Used in Hamiltonian mechanics, symplectic geometry |
Understanding Diagonal Matrices
Diagonal matrices consist of nonzero elements solely along their main diagonal, facilitating straightforward computations such as matrix multiplication and inversion. Symplectic matrices preserve a specific bilinear form essential in Hamiltonian mechanics, often involving complex block structures rather than simple diagonal forms. Understanding diagonal matrices is crucial because their simplicity allows for efficient eigenvalue determination and matrix decomposition, contrasting with the more intricate properties and roles of symplectic matrices in advanced mathematical physics.
Introduction to Symplectic Matrices
Symplectic matrices are square matrices that preserve a non-degenerate, skew-symmetric bilinear form, typically represented by the matrix J in Hamiltonian mechanics. Unlike diagonal matrices, which simplify linear transformations by scaling basis vectors independently, symplectic matrices maintain the geometric structure essential in phase space analysis. These matrices satisfy the condition \( S^T J S = J \), where \( S \) is symplectic, ensuring volume preservation and the fundamental symplectic form under transformation.
Key Properties of Diagonal Matrices
Diagonal matrices feature nonzero elements exclusively on their main diagonal, enabling straightforward operations like matrix multiplication and inversion, crucial in linear algebra and numerical analysis. Their eigenvalues are readily identified as the diagonal entries, simplifying spectral decomposition and enhancing computational efficiency in systems solving. In contrast, symplectic matrices preserve a bilinear form and maintain eigenvalue pairs, essential in Hamiltonian mechanics but lack the simple structural constraints that make diagonal matrices computationally direct.
Defining Characteristics of Symplectic Matrices
Symplectic matrices are defined by the condition \( S^T J S = J \), where \( J \) is the standard symplectic matrix, preserving the symplectic form in a \( 2n \)-dimensional vector space. Unlike diagonal matrices, which have nonzero elements only on their main diagonal, symplectic matrices maintain a structure essential for preserving volume and orientation in phase space, often characterized by block matrices satisfying \( A^T D - C^T B = I \) and \( A^T C = C^T A \). These properties are crucial in Hamiltonian mechanics and signal processing, where symplectic transformations preserve canonical commutation relations.
Mathematical Structure: Diagonal vs Symplectic
Diagonal matrices possess a simple mathematical structure characterized by nonzero elements exclusively on the main diagonal, facilitating straightforward eigenvalue computations and matrix operations. In contrast, symplectic matrices adhere to a more complex structure defined by the preservation of a skew-symmetric bilinear form, satisfying the condition \( M^T J M = J \), where \( J \) is the standard symplectic matrix. This fundamental distinction influences their applications, with diagonal matrices simplifying linear transformations and symplectic matrices playing a crucial role in Hamiltonian mechanics and symplectic geometry.
Applications of Diagonal Matrices
Diagonal matrices play a crucial role in simplifying linear transformations and are widely used in applications such as eigenvalue problems, quantum mechanics, and system stability analysis. Their structure allows for efficient matrix computations in algorithms related to image processing, signal analysis, and solving differential equations. This contrasts with symplectic matrices, which primarily appear in Hamiltonian mechanics and phase space transformations where preservation of symplectic forms is essential.
Symplectic Matrices in Physics and Engineering
Symplectic matrices are fundamental in physics and engineering due to their ability to preserve the symplectic form, ensuring the conservation of phase space volume in Hamiltonian systems. These matrices, characterized by the condition \( S^T J S = J \) where \( J \) is the standard symplectic matrix, are essential in areas such as classical mechanics, quantum mechanics, and control theory, where they maintain the structure of canonical transformations. Compared to diagonal matrices, symplectic matrices provide a more complex framework for modeling systems with intrinsic geometric and dynamical properties that cannot be captured by simple scaling transformations.
Transformations: Diagonalization and Symplectification
Diagonalization transforms a matrix into a diagonal form using eigenvalues and eigenvectors, simplifying linear transformations in Euclidean spaces. Symplectification converts a matrix into a symplectic form preserving a non-degenerate, skew-symmetric bilinear form critical in Hamiltonian mechanics. Both processes enable structural simplification but apply to distinct contexts: diagonalization in standard linear algebra and symplectification in symplectic geometry.
Comparing Advantages and Limitations
Diagonal matrices offer computational simplicity and fast eigenvalue computations due to their straightforward structure, making them ideal for problems requiring quick diagonalization and stability analysis. Symplectic matrices, essential in preserving geometric properties in Hamiltonian systems, maintain phase space volume and exhibit superior long-term numerical stability for simulations in physics and engineering. While diagonal matrices excel in speed and simplicity, symplectic matrices are indispensable for accurately modeling conservative dynamical systems despite their computational complexity.
Choosing Between Diagonal and Symplectic Approaches
Choosing between diagonal and symplectic approaches depends on the mathematical structure and application context, where diagonal methods excel in simplifying matrix computations by focusing on eigenvalue decomposition, beneficial for systems with decoupled modes. Symplectic approaches are preferred in Hamiltonian mechanics and systems preserving phase-space volume, as they maintain symplectic geometry critical for long-term stability and accurate physical modeling. Balancing computational efficiency against the need for structural preservation guides the choice, with symplectic methods favored for dynamic system simulations and diagonal methods suited for static or linearized analyses.
Diagonal Infographic
 libterm.com
libterm.com