A totally ordered group combines the algebraic structure of a group with a total order that is compatible with the group operation, meaning for any elements a, b, and c, if a <= b, then ac <= bc and ca <= cb. This ordering allows for well-defined comparisons across all elements, enabling analysis of their algebraic and order-theoretic properties simultaneously. Explore the rest of this article to understand how totally ordered groups are constructed and applied in various mathematical fields.
Table of Comparison
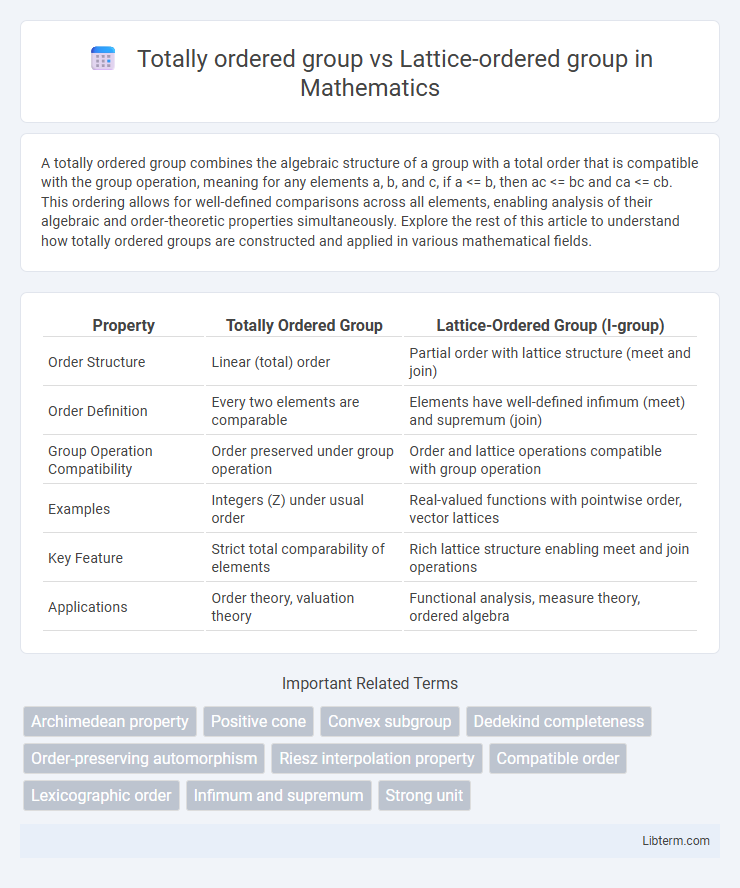
| Property | Totally Ordered Group | Lattice-Ordered Group (l-group) |
|---|---|---|
| Order Structure | Linear (total) order | Partial order with lattice structure (meet and join) |
| Order Definition | Every two elements are comparable | Elements have well-defined infimum (meet) and supremum (join) |
| Group Operation Compatibility | Order preserved under group operation | Order and lattice operations compatible with group operation |
| Examples | Integers (Z) under usual order | Real-valued functions with pointwise order, vector lattices |
| Key Feature | Strict total comparability of elements | Rich lattice structure enabling meet and join operations |
| Applications | Order theory, valuation theory | Functional analysis, measure theory, ordered algebra |
Introduction to Ordered Groups
Totally ordered groups are algebraic structures where the group elements are arranged in a linear order compatible with the group operation, meaning every pair of elements is comparable. Lattice-ordered groups (l-groups) extend this concept by incorporating a lattice structure that allows for the existence of suprema and infima for every pair of elements, enhancing the group's ability to model partial orders and complex hierarchies. These foundational differences play a crucial role in the study of ordered groups, influencing their algebraic properties and applications in fields such as functional analysis and group theory.
Defining Totally Ordered Groups
A totally ordered group is a group equipped with a total order compatible with the group operation, meaning for any elements a, b, and c, if a <= b, then both ca <= cb and ac <= bc hold. This total order ensures a linear or chain-like structure, where every pair of elements is comparable, unlike lattice-ordered groups, which allow for partial ordering with meet and join operations. The compatibility of the total order with the group operation is crucial for analyzing algebraic and order-theoretic properties in totally ordered groups.
Understanding Lattice-Ordered Groups
Lattice-ordered groups (l-groups) extend totally ordered groups by allowing each pair of elements to have both a least upper bound and a greatest lower bound, forming a lattice structure compatible with the group operation. In l-groups, the order is partial rather than total, enabling more complex interactions between elements while preserving group properties. Understanding l-groups involves studying how lattice operations interact with group multiplication and inversion, with applications in algebra and functional analysis.
Key Structural Differences
Totally ordered groups possess a linear order where every pair of elements is comparable, ensuring that the group operation respects this total order. Lattice-ordered groups (l-groups), in contrast, have a partially ordered set with a lattice structure allowing for the existence of both least upper bounds (joins) and greatest lower bounds (meets) for any two elements. Unlike totally ordered groups, l-groups accommodate more complex orderings where elements may be incomparable, but their lattice operations provide a richer algebraic framework for order manipulation.
Order Properties and Implications
Totally ordered groups possess a linear order where every pair of elements is comparable, ensuring straightforward order properties and enabling direct comparability in algebraic operations. Lattice-ordered groups, by contrast, feature a partial order with meets and joins for every pair of elements, supporting a more complex structure that accommodates both supremum and infimum. This distinction impacts implications such as the ability to define absolute values in lattice-ordered groups, while totally ordered groups benefit from simpler order-driven algorithms and decision processes.
Examples of Totally Ordered Groups
Examples of totally ordered groups include the group of integers (Z, +) with the natural order, the group of real numbers (R, +) under the usual order, and the lexicographic order on the direct product Z x Z. These groups are characterized by a total order compatible with the group operation, where every pair of elements is comparable. In contrast, lattice-ordered groups (l-groups) require the existence of suprema and infima for every pair of elements, allowing partial orders that are not necessarily total.
Examples of Lattice-Ordered Groups
Lattice-ordered groups (l-groups) include important examples such as the group of real numbers under addition with the usual order, where the lattice operations correspond to minimum and maximum functions. Another key example is the group of continuous real-valued functions on a compact space, ordered pointwise, forming an l-group with lattice operations defined pointwise. These examples illustrate the rich order-theoretic structure of l-groups, distinguishing them from totally ordered groups where the order is linear rather than lattice-based.
Applications in Mathematics and Beyond
Totally ordered groups provide a linear ordering compatible with group operations, facilitating applications in algebraic number theory and decision-making frameworks. Lattice-ordered groups, possessing a lattice structure that allows the definition of joins and meets, are essential in functional analysis, optimization, and economics for modeling resource allocation and preference relations. Both structures underpin advancements in mathematical logic, topology, and theoretical computer science by enabling complex order-theoretic and algebraic analysis.
Relationships and Intersections
Totally ordered groups (TOGs) are algebraic structures where every pair of elements is comparable, ensuring a linear order compatible with the group operation. Lattice-ordered groups (l-groups) generalize TOGs by requiring a partial order where every pair of elements has a greatest lower bound and least upper bound, forming a lattice structure consistent with group operations. The intersection lies in the fact that every totally ordered group is a lattice-ordered group with a linear lattice, but not every lattice-ordered group is totally ordered due to the absence of comparability between all elements.
Summary and Further Reading
Totally ordered groups are algebraic structures where every pair of elements is comparable, forming a linear order compatible with the group operation, whereas lattice-ordered groups (l-groups) generalize this by allowing the group elements to form a lattice structure with both meet and join operations. Both concepts are fundamental in order theory and algebra, with totally ordered groups often serving as simpler models for studying order properties, while l-groups provide richer frameworks applicable in functional analysis and ring theory. For further reading, consider exploring "Partially Ordered Algebraic Systems" by F.S. Anderson and "Lattice-Ordered Groups: An Introduction" by Margaret T. Morley, which offer comprehensive treatments of order structures in algebra.
Totally ordered group Infographic
 libterm.com
libterm.com