Satisfiability is a fundamental concept in logic and computer science, referring to the problem of determining if there exists an assignment of truth values that makes a given logical formula true. Understanding satisfiability is crucial for solving complex computational problems, including those in automated reasoning, verification, and artificial intelligence. Explore the rest of the article to learn how satisfiability impacts your computational tasks and techniques to effectively approach it.
Table of Comparison
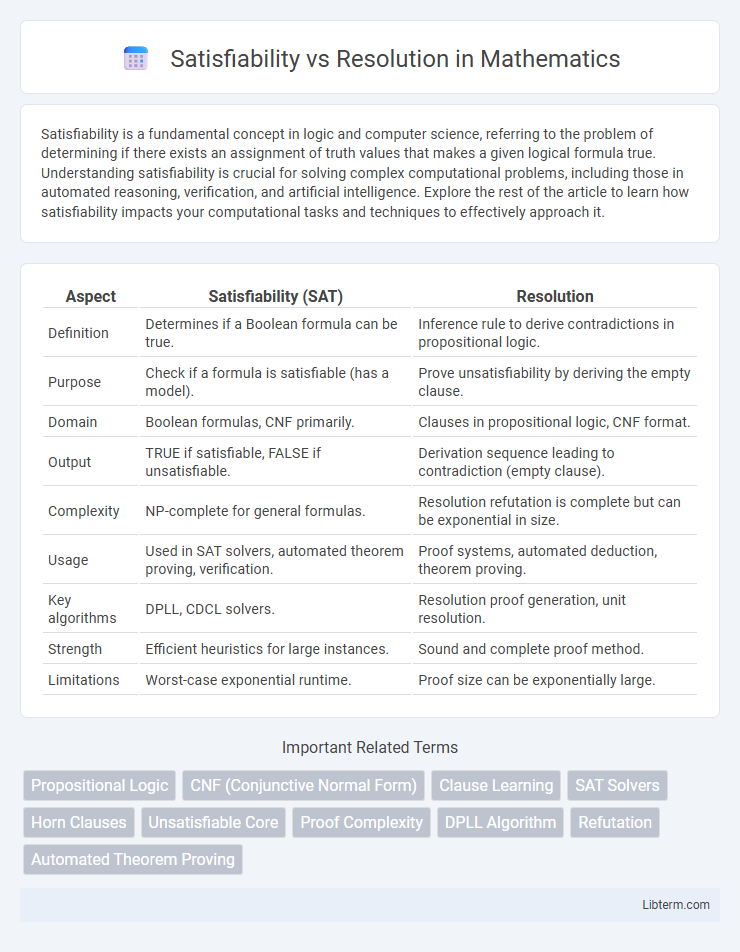
| Aspect | Satisfiability (SAT) | Resolution |
|---|---|---|
| Definition | Determines if a Boolean formula can be true. | Inference rule to derive contradictions in propositional logic. |
| Purpose | Check if a formula is satisfiable (has a model). | Prove unsatisfiability by deriving the empty clause. |
| Domain | Boolean formulas, CNF primarily. | Clauses in propositional logic, CNF format. |
| Output | TRUE if satisfiable, FALSE if unsatisfiable. | Derivation sequence leading to contradiction (empty clause). |
| Complexity | NP-complete for general formulas. | Resolution refutation is complete but can be exponential in size. |
| Usage | Used in SAT solvers, automated theorem proving, verification. | Proof systems, automated deduction, theorem proving. |
| Key algorithms | DPLL, CDCL solvers. | Resolution proof generation, unit resolution. |
| Strength | Efficient heuristics for large instances. | Sound and complete proof method. |
| Limitations | Worst-case exponential runtime. | Proof size can be exponentially large. |
Introduction to Satisfiability and Resolution
Satisfiability (SAT) refers to the problem of determining if there exists an assignment of truth values to variables that makes a given Boolean formula true. Resolution is an inference rule used in logic and automated theorem proving to derive new clauses and determine the satisfiability of propositional formulas by refutation. Both concepts are fundamental in fields such as artificial intelligence, formal verification, and computational logic, where solving SAT problems efficiently is crucial for optimization and reasoning tasks.
Defining Satisfiability in Logic
Satisfiability in logic refers to the property of a logical formula to have at least one interpretation or assignment of truth values that makes the formula true. It is a fundamental concept in propositional and predicate logic, often investigated through satisfiability solvers that determine whether such assignments exist. Understanding satisfiability is crucial for fields like automated theorem proving, where determining the satisfiability of a logical expression can prove or disprove the validity of arguments.
Understanding Resolution in Automated Reasoning
Resolution is a fundamental inference rule used in automated reasoning to determine the satisfiability of propositional logic formulas. It operates by refuting the negation of a formula through iterative application of the resolution rule on clauses, deriving the empty clause to confirm unsatisfiability. This method efficiently handles CNF (Conjunctive Normal Form) representations, enabling automated theorem provers to systematically infer contradictions and thus prove or disprove logical statements.
Core Differences Between Satisfiability and Resolution
Satisfiability (SAT) involves determining if there exists an assignment of truth values to variables that makes a propositional formula true, focusing on solution existence. Resolution is a proof technique used to derive contradictions by systematically combining clauses, enabling automated theorem proving and refutation in propositional logic. The core difference lies in SAT's goal of finding a satisfying assignment, while resolution seeks to prove unsatisfiability by deriving an empty clause.
Role of Satisfiability in Propositional Logic
Satisfiability in propositional logic determines whether there exists an assignment of truth values to variables that makes a formula true, serving as a foundational concept in automated theorem proving and artificial intelligence. It directly impacts the efficiency of solving complex logical formulas, as satisfiability checks underpin decision procedures and constraint satisfaction problems. Algorithms like SAT solvers exploit satisfiability to handle large-scale propositional formulas, enabling practical applications in verification, planning, and optimization tasks.
Resolution as an Inference Mechanism
Resolution is a fundamental inference mechanism in automated theorem proving and logic programming, used to determine the satisfiability of propositional and first-order logic formulas. By iteratively applying the resolution rule to a set of clauses, it derives contradictions that indicate unsatisfiability, thereby proving the original formula's validity. This approach leverages refutation completeness, making resolution a cornerstone technique in satisfiability checking and logical inference systems.
Applications of Satisfiability in Computer Science
Satisfiability (SAT) plays a crucial role in computer science applications such as automated theorem proving, hardware and software verification, and artificial intelligence for constraint solving and planning. SAT solvers efficiently determine the satisfiability of logical formulas, enabling optimization in model checking and bug detection within complex systems. Unlike resolution methods that primarily focus on proof generation, SAT-based techniques offer scalable solutions widely adopted in formal methods and combinatorial problem solving.
Practical Uses of Resolution in Problem Solving
Resolution is widely applied in automated theorem proving and logic programming due to its ability to systematically derive contradictions and validate logical statements. Its practical use extends to solving complex problems in artificial intelligence, such as knowledge representation, where it enables efficient inference by simplifying propositional and first-order logic expressions. Resolution's structured approach aids in debugging software specifications and verifying hardware circuits, making it indispensable for ensuring the correctness and reliability of systems.
Satisfiability vs Resolution: Strengths and Limitations
Satisfiability (SAT) solvers excel in handling large and complex boolean formulae, offering efficient solutions through advanced heuristics and conflict-driven clause learning, making them ideal for practical problem-solving in verification and AI. Resolution methods provide a complete and sound inference mechanism rooted in propositional logic, valuable for formal proofs but often hindered by exponential growth in intermediate clauses, limiting scalability. While SAT solvers emphasize performance and scalability, resolution focuses on proof-theoretic clarity, balancing practical efficiency against rigorous logical deduction.
Future Developments in Satisfiability and Resolution Techniques
Future developments in satisfiability and resolution techniques are centered around enhancing algorithmic efficiency and scalability for complex problem instances in artificial intelligence and formal verification. Innovations include integrating machine learning to guide search heuristics, optimizing clause learning strategies, and exploiting parallel and distributed computing architectures. These advances aim to handle larger, more intricate formulas while reducing computational overhead, significantly impacting automated reasoning and combinatorial optimization domains.
Satisfiability Infographic
 libterm.com
libterm.com