Subdual refers to the act of overcoming resistance or control over a person, group, or situation, often through force or persuasion. Effective techniques for subdual can vary depending on the context, such as law enforcement, conflict resolution, or personal discipline. Discover the essential strategies and insights behind subdual to enhance your understanding and application in different scenarios.
Table of Comparison
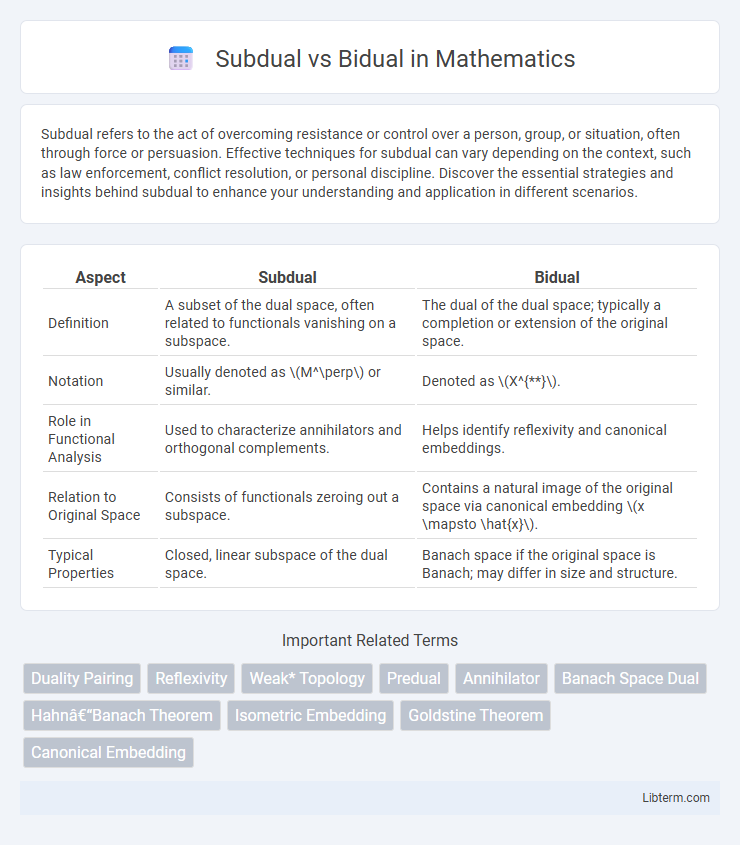
| Aspect | Subdual | Bidual |
|---|---|---|
| Definition | A subset of the dual space, often related to functionals vanishing on a subspace. | The dual of the dual space; typically a completion or extension of the original space. |
| Notation | Usually denoted as \(M^\perp\) or similar. | Denoted as \(X^{}\). |
| Role in Functional Analysis | Used to characterize annihilators and orthogonal complements. | Helps identify reflexivity and canonical embeddings. |
| Relation to Original Space | Consists of functionals zeroing out a subspace. | Contains a natural image of the original space via canonical embedding \(x \mapsto \hat{x}\). |
| Typical Properties | Closed, linear subspace of the dual space. | Banach space if the original space is Banach; may differ in size and structure. |
Introduction to Subdual and Bidual
Subdual and bidual spaces are fundamental concepts in functional analysis, specifically within the study of Banach spaces. The subdual of a Banach space X refers to a subset of the dual space X* that contains functionals representing certain restricted evaluation properties, while the bidual space X is the dual of the dual space X*, capturing a larger structure that often includes X as a dense embedded subspace. Understanding the relationship between X, its dual X*, and its bidual X provides critical insights into reflexivity and the extension of linear functionals in normed vector spaces.
Definitions: Understanding Subdual
Subdual involves the process of capturing and controlling a space but not necessarily fixing or closing it completely, often used in topological vector spaces to describe a weaker form of convergence. It contrasts with bidual, which refers to the dual of the dual space, encapsulating the space of all continuous linear functionals on the dual space itself. Understanding subdual is essential for analyzing reflexivity and weak topologies in functional analysis, where subdual spaces play a role in characterizing dual pairings and continuity conditions.
Definitions: Exploring Bidual
Bidual refers to the dual of the dual space of a given vector space, often denoted as \(X^{}\), where \(X^*\) is the dual space consisting of all continuous linear functionals on \(X\). The bidual space plays a crucial role in functional analysis, serving as an extension that may embed the original space \(X\) as a subspace, typically via the canonical embedding mapping each element to its evaluation functional. Understanding the bidual is essential for exploring reflexivity of Banach spaces and analyzing the properties of linear operators and duality mappings.
Mathematical Contexts of Subdual and Bidual
In mathematical contexts, the subdual typically refers to a subset of the dual space that preserves certain structural properties or constraints, such as positivity or continuity, within functional analysis or convex analysis. The bidual extends this idea by considering the dual of the dual space, often revealing reflexivity properties and enabling the representation of elements through canonical embeddings, which is pivotal in Banach space theory. Understanding the relationship between subdual and bidual spaces aids in analyzing the completeness and compactness of functional spaces, critical in optimization and operator theory.
Differences Between Subdual and Bidual
The subdual of a vector space consists of all functionals that vanish on a specified subspace, while the bidual involves the dual of the dual space, often providing a natural embedding of the original space. Subduals highlight constraints related to specific subspaces, whereas biduals emphasize the reflexivity and extension of linear functionals. The key difference lies in subduals being subspaces of the dual space, contrasted with biduals as spaces of functionals acting on the dual, encapsulating higher-order duality.
Importance in Functional Analysis
Subdual and bidual spaces play a crucial role in functional analysis by providing deeper insight into the structure of Banach spaces and their duals. The subdual space captures norm-attaining functionals, facilitating the study of weak* topologies and compactness properties, while the bidual space extends a Banach space to a reflexive environment, enabling powerful representation theorems and the analysis of extensions of linear operators. Understanding the interplay between subdual and bidual spaces is essential for characterizing reflexivity, weak compactness, and duality mappings in infinite-dimensional spaces.
Applications in Vector Spaces
Subdual and bidual spaces are critical in functional analysis, particularly in the study of vector spaces and their duals. The subdual relates to a selected subset of the dual space, often focusing on specific functionals, while the bidual is the dual of the dual space, capturing a broader spectrum of linear functionals and embedding the original space via canonical mapping. Applications in reflexivity and operator theory leverage the bidual to understand continuity and compactness properties, whereas subdual spaces play roles in optimizing functional constraints within vector space frameworks.
Common Examples and Use Cases
Subduals and biduals appear frequently in functional analysis, especially in the study of Banach spaces. Common examples include the space \( \ell^1 \), whose dual is \( \ell^\infty \) and bidual is more extensive, highlighting reflexivity properties; similarly, \( L^p \) spaces with \( 1 < p < \infty \) exhibit isometric isomorphisms between the space and its bidual. Use cases focus on understanding the reflexivity of spaces, extensions of operators, and duality mappings critical for optimization problems and advanced PDE analysis.
Challenges and Limitations
Subduals often face challenges in maintaining robust communication and coordination, leading to inefficiencies in decision-making processes. Bidual frameworks encounter limitations related to increased complexity and resource allocation, which can hinder scalability and operational effectiveness. Both models struggle with balancing flexibility and control, impacting overall system adaptability and performance.
Conclusion: Choosing Between Subdual and Bidual
Choosing between subdual and bidual spaces depends on the specific goals of functional analysis or optimization problems. Subdual spaces offer a more manageable framework with fewer topological complications, ideal for practical applications and computational methods. Bidual spaces provide a richer, more complete structure that is valuable in theoretical contexts requiring reflexivity or the study of weak* topologies.
Subdual Infographic
 libterm.com
libterm.com