Discover how our innovative product enhances your daily routine with cutting-edge technology and user-friendly design. Engineered for efficiency and durability, it seamlessly integrates into your lifestyle, delivering unmatched performance and reliability. Explore the full article to learn how this product can transform your experience and meet your needs effortlessly.
Table of Comparison
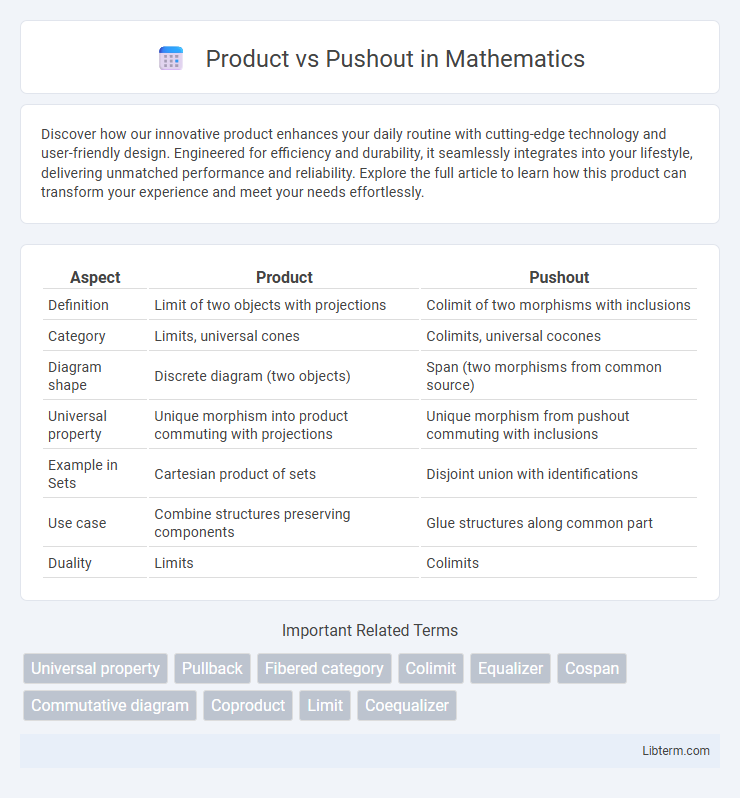
| Aspect | Product | Pushout |
|---|---|---|
| Definition | Limit of two objects with projections | Colimit of two morphisms with inclusions |
| Category | Limits, universal cones | Colimits, universal cocones |
| Diagram shape | Discrete diagram (two objects) | Span (two morphisms from common source) |
| Universal property | Unique morphism into product commuting with projections | Unique morphism from pushout commuting with inclusions |
| Example in Sets | Cartesian product of sets | Disjoint union with identifications |
| Use case | Combine structures preserving components | Glue structures along common part |
| Duality | Limits | Colimits |
Introduction to Product vs Pushout
Product and pushout are fundamental concepts in category theory used to describe universal properties of objects and morphisms. A product combines two objects into a single object with projection maps that uniquely factorize any morphism into each component, reflecting a categorical notion of conjunction. Pushouts, dual to pullbacks, amalgamate two objects over a common subobject, providing a universal construction for co-limits and modeling the notion of gluing in various mathematical contexts.
Defining Product in Mathematics
In mathematics, a product refers to a universal construction that combines two objects into a pair, capturing their structural relationship via projection maps. Unlike pushouts, which amalgamate objects along a shared substructure, products focus on the simultaneous presence of multiple components without imposing identifications. Products are fundamental in category theory for building new objects that represent the Cartesian product of sets, groups, or other algebraic structures.
Understanding Pushout: A Categorical Perspective
Pushouts in category theory represent a universal construction that amalgamates two morphisms with a common domain into a single object, generalizing the notion of "gluing" structures along shared subparts. Unlike product objects, which capture simultaneous relations by pairing objects, pushouts serve to identify and merge overlapping components, formalized through a commutative square that satisfies a universal property. Understanding pushouts enables rigorous modeling of colimits, providing critical insights into the structure and behavior of categorical diagrams beyond mere product formations.
Key Differences Between Product and Pushout
The key differences between product and pushout lie in their categorical roles: a product represents a limit that combines two objects via projection maps, whereas a pushout is a colimit that merges two objects along a shared subobject through injection maps. Products enforce universal properties through unique morphisms factoring into the product, while pushouts use universal properties to unite objects by identifying common parts. These distinctions highlight how products preserve structure via projections, and pushouts create new objects by gluing along morphisms.
Visualizing Product and Pushout with Diagrams
Visualizing product and pushout in category theory involves distinct diagrammatic representations: the product is depicted as a cone with morphisms projecting onto each factor, often shown as two arrows converging from an object to two others. In contrast, the pushout is represented by a cocone diagram where two morphisms share a common domain and merge into a universal object via a coequalizing square. These diagrams aid in understanding universal properties, highlighting the product as a limit and the pushout as a colimit in categorical constructions.
Real-World Examples of Product and Pushout
In category theory, product and pushout serve distinct roles exemplified in various real-world scenarios. Product models simultaneous conditions, such as combining a smartphone's camera and battery performance to evaluate overall user satisfaction. Pushout represents a unification process, like merging two software branches in version control to consolidate features and resolve conflicts into a new unified codebase.
Applications of Product in Various Fields
The product operation in mathematics and computer science plays a crucial role in fields such as database theory, where it models join operations for combining datasets, and in category theory, underpinning the structure of Cartesian products essential for constructing complex systems. In computer graphics, the product operation helps in defining transformations and combining geometric objects for rendering scenes. Its applicability extends to network theory for analyzing interconnected systems and to machine learning for feature space construction and tensor operations, highlighting its versatility across diverse scientific and engineering domains.
Pushout Usage Scenarios in Algebra and Topology
Pushouts serve critical roles in algebra and topology, particularly in constructing new objects by amalgamating two spaces or structures along a shared substructure. In topology, pushouts are instrumental in forming quotient spaces, attaching cells, and modeling gluing processes, facilitating the study of complex spaces via simpler components. Algebraically, pushouts enable the combination of groups, rings, or modules over a common subobject, supporting the formulation of colimits and completing diagrams in category theory.
Common Misconceptions About Product and Pushout
Common misconceptions about Product and Pushout often arise from confusing their categorical roles; a Product represents a universal limit that combines objects through projections, while a Pushout is a universal colimit merging morphisms via injections. Many mistakenly assume Products and Pushouts are symmetric operations or interchangeable, overlooking that Products model "and" relationships (limits) whereas Pushouts model "or" relationships (colimits) in category theory. Understanding their distinct universal properties and directional constructs is essential to avoid misapplication in mathematical and computational contexts.
Conclusion: Choosing Between Product and Pushout
Choosing between product and pushout in category theory depends on the nature of the problem and desired universal property; products provide a universal object with projections preserving individual structures, while pushouts construct a new object by amalgamating data along shared morphisms. In practice, products are optimal for combining independent structures, whereas pushouts are essential for identifying and merging diagrams via common subobjects. Understanding the categorical context and the role of limits or colimits guides the effective selection between these fundamental constructions.
Product Infographic
 libterm.com
libterm.com