Elliptic functions are complex functions characterized by their double periodicity, exhibiting two distinct periods in the complex plane. These functions play a crucial role in various fields, including number theory, algebraic geometry, and mathematical physics, due to their rich structure and applications. Discover how elliptic functions influence modern mathematics and uncover their fascinating properties in the rest of this article.
Table of Comparison
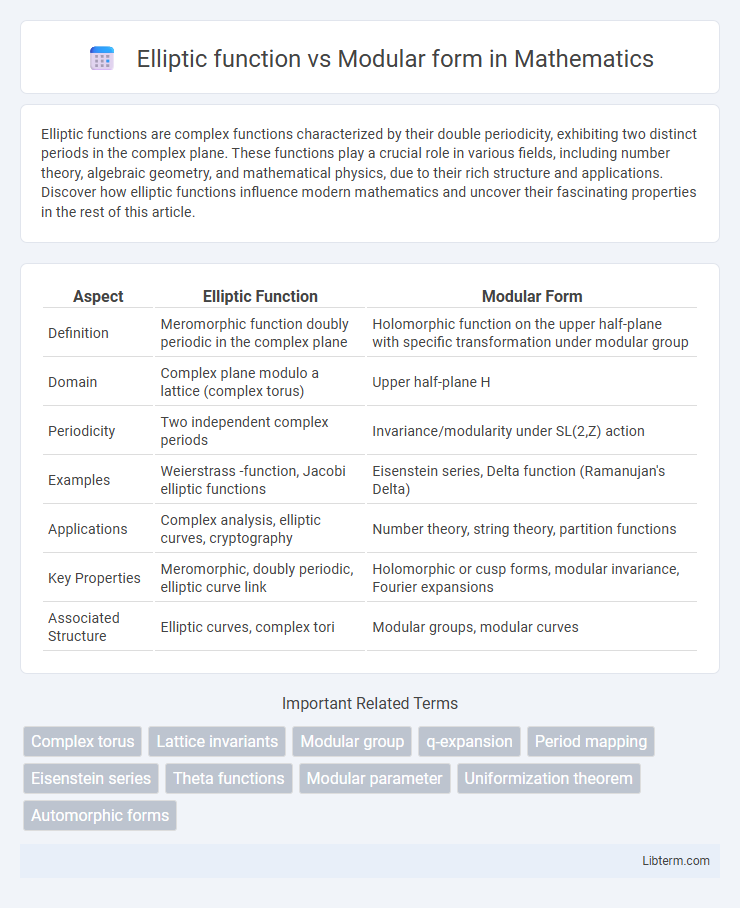
| Aspect | Elliptic Function | Modular Form |
|---|---|---|
| Definition | Meromorphic function doubly periodic in the complex plane | Holomorphic function on the upper half-plane with specific transformation under modular group |
| Domain | Complex plane modulo a lattice (complex torus) | Upper half-plane H |
| Periodicity | Two independent complex periods | Invariance/modularity under SL(2,Z) action |
| Examples | Weierstrass -function, Jacobi elliptic functions | Eisenstein series, Delta function (Ramanujan's Delta) |
| Applications | Complex analysis, elliptic curves, cryptography | Number theory, string theory, partition functions |
| Key Properties | Meromorphic, doubly periodic, elliptic curve link | Holomorphic or cusp forms, modular invariance, Fourier expansions |
| Associated Structure | Elliptic curves, complex tori | Modular groups, modular curves |
Introduction to Elliptic Functions and Modular Forms
Elliptic functions are complex functions characterized by their double periodicity and arise naturally from the inversion of elliptic integrals, forming a fundamental class in complex analysis. Modular forms are holomorphic functions on the upper half-plane that transform in specific ways under the action of the modular group, encoding deep arithmetic and geometric information. The interplay between elliptic functions and modular forms is central to number theory, with modular forms providing powerful tools for studying the properties and symmetries of elliptic functions.
Historical Development and Mathematical Context
Elliptic functions originated in the 19th century through the work of mathematicians like Niels Henrik Abel and Carl Gustav Jacobi, who studied inverse functions of elliptic integrals and established doubly periodic complex functions. Modular forms emerged later, notably developed by Ernst Eduard Kummer and Felix Klein, as complex analytic functions exhibiting specific transformation properties under the modular group action on the upper half-plane, connecting deeply to number theory and arithmetic geometry. Both concepts intersect in the theory of elliptic curves, with modular forms playing a crucial role in understanding elliptic functions' symmetries and modularity, exemplified by the proof of Fermat's Last Theorem through modularity lifting theorems.
Defining Elliptic Functions
Elliptic functions are meromorphic functions characterized by their double periodicity, defined on the complex plane with two distinct periods forming a lattice. They generalize trigonometric functions by extending periodicity in two directions, fundamental in complex analysis and number theory. Modular forms, by contrast, are holomorphic functions on the upper half-plane that transform in specific ways under the modular group, closely related to the lattice structures defining elliptic functions.
Properties and Applications of Elliptic Functions
Elliptic functions are meromorphic functions characterized by double periodicity, meaning they repeat values in two distinct lattice directions, which distinguishes them from modular forms that are holomorphic on the upper half-plane and invariant under modular transformations. Key properties of elliptic functions include their complex lattice structure, residue theorems, and relation to elliptic curves, making them essential in number theory and complex analysis. Applications of elliptic functions span cryptography, particularly in elliptic curve cryptography (ECC), and solutions to nonlinear differential equations, highlighting their significance in both theoretical and applied mathematics.
Modular Forms: Definition and Key Characteristics
Modular forms are complex analytic functions defined on the upper half-plane that satisfy specific transformation properties under the action of the modular group \( \text{SL}_2(\mathbb{Z}) \). These functions exhibit modular symmetry and possess Fourier expansions, allowing them to encode deep arithmetic information such as the coefficients related to elliptic curves and number theory. Key characteristics include holomorphy, modular invariance, and growth conditions at cusps, making modular forms fundamental objects in modern mathematics and cryptography.
Fundamental Differences Between Elliptic Functions and Modular Forms
Elliptic functions are meromorphic functions defined on the complex plane that are doubly periodic, exhibiting invariance under translations by elements of a lattice, while modular forms are holomorphic functions on the upper half-plane exhibiting specific transformation properties under the action of the modular group SL(2,Z). Elliptic functions have poles within their fundamental parallelogram and relate directly to complex tori, whereas modular forms are characterized by their q-expansion and growth conditions at cusps, often encoding arithmetic information. The core distinction lies in elliptic functions' geometric periodicity versus modular forms' arithmetic symmetries and modular invariance.
Connections and Interactions in Mathematics
Elliptic functions and modular forms are deeply intertwined through their roles in complex analysis and number theory, as elliptic functions, defined by doubly periodic meromorphic functions, correspond to lattices in the complex plane, while modular forms arise as functions on the upper half-plane with transformation properties related to the modular group. The connection is exemplified by the j-invariant, a modular function that classifies elliptic curves up to isomorphism, linking the theory of elliptic functions to modular forms and enabling applications in arithmetic geometry and string theory. This interaction facilitates the translation of geometric properties of elliptic curves into the analytic framework of modular forms, enriching the understanding of both objects in advanced mathematical research.
Notable Theorems Involving Both Concepts
The Modularity Theorem, formerly known as the Taniyama-Shimura-Weil conjecture, establishes a profound link between elliptic curves over the rationals and modular forms by demonstrating that every elliptic curve corresponds to a modular form. The Eichler-Shimura relation connects Hecke operators acting on modular forms to the cohomology of modular curves, which are closely related to the theory of elliptic functions. Complex multiplication theory further intertwines elliptic functions and modular forms by describing special elliptic curves whose L-functions can be expressed via modular forms with CM, highlighting deep arithmetic and analytic connections.
Applications in Number Theory and Cryptography
Elliptic functions provide a framework for understanding complex tori and are instrumental in the study of elliptic curves, which underpin modern cryptographic systems such as Elliptic Curve Cryptography (ECC) due to their efficiency and security. Modular forms, characterized by their transformation properties under the modular group, play a crucial role in number theory through their connection to L-functions and the proof of Fermat's Last Theorem via the modularity theorem. The interplay between elliptic functions and modular forms fosters advancements in integer factorization, primality testing, and secure key exchange protocols, making them foundational tools in both theoretical and applied cryptography.
Conclusion: Future Directions and Open Problems
Future research on elliptic functions and modular forms centers on deepening the understanding of their interconnected structures within number theory and algebraic geometry. Key open problems include exploring the Langlands program's implications for modular forms and the characterization of elliptic curves over various fields. Advances in computational methods and the theory of automorphic forms promise to unveil new applications in cryptography and mathematical physics.
Elliptic function Infographic
 libterm.com
libterm.com