Pullbacks represent a temporary reversal in the price of an asset within an overall uptrend, providing traders with opportunities to enter the market at a better price. Understanding pullback patterns and key support levels can help you manage risk and enhance your trading strategy. Explore the rest of the article to learn how to identify and capitalize on pullbacks effectively.
Table of Comparison
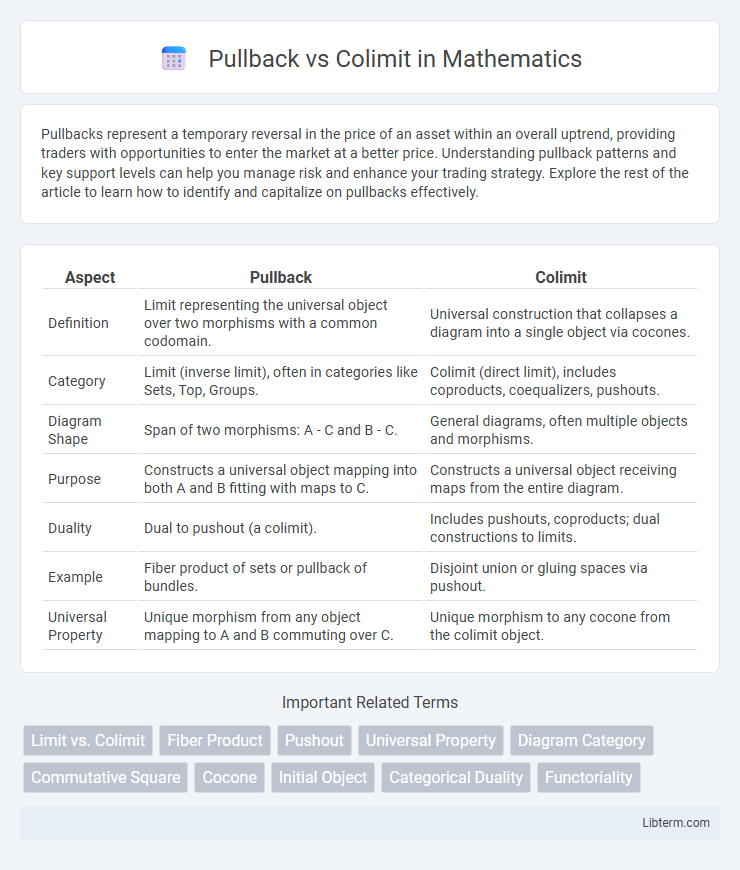
| Aspect | Pullback | Colimit |
|---|---|---|
| Definition | Limit representing the universal object over two morphisms with a common codomain. | Universal construction that collapses a diagram into a single object via cocones. |
| Category | Limit (inverse limit), often in categories like Sets, Top, Groups. | Colimit (direct limit), includes coproducts, coequalizers, pushouts. |
| Diagram Shape | Span of two morphisms: A - C and B - C. | General diagrams, often multiple objects and morphisms. |
| Purpose | Constructs a universal object mapping into both A and B fitting with maps to C. | Constructs a universal object receiving maps from the entire diagram. |
| Duality | Dual to pushout (a colimit). | Includes pushouts, coproducts; dual constructions to limits. |
| Example | Fiber product of sets or pullback of bundles. | Disjoint union or gluing spaces via pushout. |
| Universal Property | Unique morphism from any object mapping to A and B commuting over C. | Unique morphism to any cocone from the colimit object. |
Introduction to Pullbacks and Colimits
Pullbacks are a specific type of limit in category theory that represent the universal solution to the problem of finding an object mapping to two given objects with a common codomain, effectively generalizing the notion of fibered products. Colimits, on the other hand, encompass a broader class of constructions including coproducts, coequalizers, and pushouts, serving as universal objects that coalesce diagrams in a category. Understanding the fundamental definitions and examples of pullbacks and colimits is crucial for exploring their roles in constructing and analyzing categorical limits and colimits in various mathematical contexts.
Fundamental Concepts in Category Theory
Pullbacks and colimits are fundamental constructions in category theory used to define limits and universal properties. A pullback is a type of limit representing the universal solution to a pair of morphisms with a common codomain, often visualized as a fiber product, ensuring commutativity and universality in diagrams. Colimits, including pushouts and coproducts, are dual notions describing universal objects coalescing diagrams via cocones, capturing the essence of "gluing" or amalgamating objects and morphisms in a category.
Defining Pullbacks: Structure and Properties
Pullbacks are defined as the limit of a diagram consisting of two morphisms with a common codomain, forming a universal construction that captures the fibered product in category theory. This structure consists of an object paired with two projection morphisms satisfying a universal property, ensuring any other object with morphisms factoring through the original diagram uniquely factors through the pullback. The pullback preserves properties such as commutativity and universality, making it a fundamental tool for constructing and analyzing limits in various categorical contexts.
Understanding Colimits: Types and Examples
Colimits in category theory generalize constructions like coproducts, pushouts, and direct limits, serving as universal cocones from a diagram to a single object. Types of colimits include coproducts that combine objects disjointly, pushouts that amalgamate objects along a shared subobject, and coequalizers that identify morphisms, each illustrating a distinctive way of "gluing" or unifying structures. Examples include the pushout used in topological spaces to construct spaces by identifying subspaces, or the coproduct in sets forming disjoint unions, demonstrating the colimit's versatility in synthesizing objects from diagrams.
Key Differences Between Pullbacks and Colimits
Pullbacks represent a specific type of limit describing the universal solution to two morphisms with a common codomain, typically used to construct fibered products in category theory. Colimits generalize the notion of "gluing" objects along diagrams, capturing universal constructions such as coproducts, coequalizers, and pushouts that combine objects by identifying morphisms. The key difference lies in pullbacks being limits focusing on the intersection of structures, while colimits are colimits focusing on the aggregation or amalgamation of structures.
Visual Representations in Diagrams
Pullbacks are visualized as a commutative square diagram that represents the limit of two morphisms converging to a common codomain, emphasizing their universal property through the apex object connecting both paths. Colimits appear as cocommutative diagrams forming a co-cone, typically represented by pushout squares or coproduct diagrams that unify objects via injections, highlighting the universal property of amalgamation. Diagrammatic clarity in pullbacks shows object intersections, whereas colimit diagrams emphasize object amalgamations and identification processes.
Applications of Pullbacks in Mathematics
Pullbacks serve as a crucial tool in category theory to construct universal solutions for fibered products, ensuring compatibility and commutativity of diagrams in various mathematical contexts. They find applications in algebraic geometry for defining fiber products of schemes, in homological algebra for defining limits of chain complexes, and in topology for constructing pullback bundles and fibered spaces. The categorical pullback captures the essence of inverse image constructions, making it instrumental in structuring and analyzing complex mathematical objects.
Practical Uses of Colimits in Various Fields
Colimits play a crucial role in fields like algebraic topology, where they help construct spaces by gluing simpler components, and in computer science, particularly in type theory and the semantics of programming languages, for combining data types or processes. In category theory, colimits generalize notions of unions, quotients, and direct limits, enabling practical modeling of complex systems and data integration tasks. Compared to pullbacks, which focus on limits and fibered products, colimits facilitate synthesis and aggregation, making them essential for applications requiring the merging or coalescing of structures.
Choosing Between Pullbacks and Colimits
Choosing between pullbacks and colimits depends on the categorical context and the type of construction needed: pullbacks are used to find universal objects that represent fibered products or intersections, essential in defining limits over diagrams with two morphisms sharing a codomain. Colimits, on the other hand, capture universal cocones typically used to amalgamate objects along shared structures, such as in pushouts or coequalizers, facilitating the construction of quotients or unions. When the goal is to unify data by gluing along common parts, colimits are appropriate; for querying refined intersections or consistent data fitting, pullbacks offer precise structural insight.
Summary and Future Directions
Pullbacks serve as a fundamental construction in category theory, representing the limit of two morphisms with a common codomain, while colimits generalize the concept of gluing objects together along specified morphisms. Future directions include exploring higher-dimensional category theory to analyze pullbacks and colimits in -categories, and applying these concepts to enhance compositionality in homotopy theory, type theory, and algebraic geometry. Advances in computational category theory aim to develop efficient algorithms for calculating pullbacks and colimits in large and complex categorical structures.
Pullback Infographic
 libterm.com
libterm.com