Unique Factorization Domain (UFD) is a type of integral domain where every element can be uniquely factored into irreducible elements, up to order and units. This property ensures consistent factorization results, making UFDs fundamental in algebraic number theory and polynomial rings. Explore the rest of the article to understand how UFDs influence modern mathematical structures and your problem-solving approach.
Table of Comparison
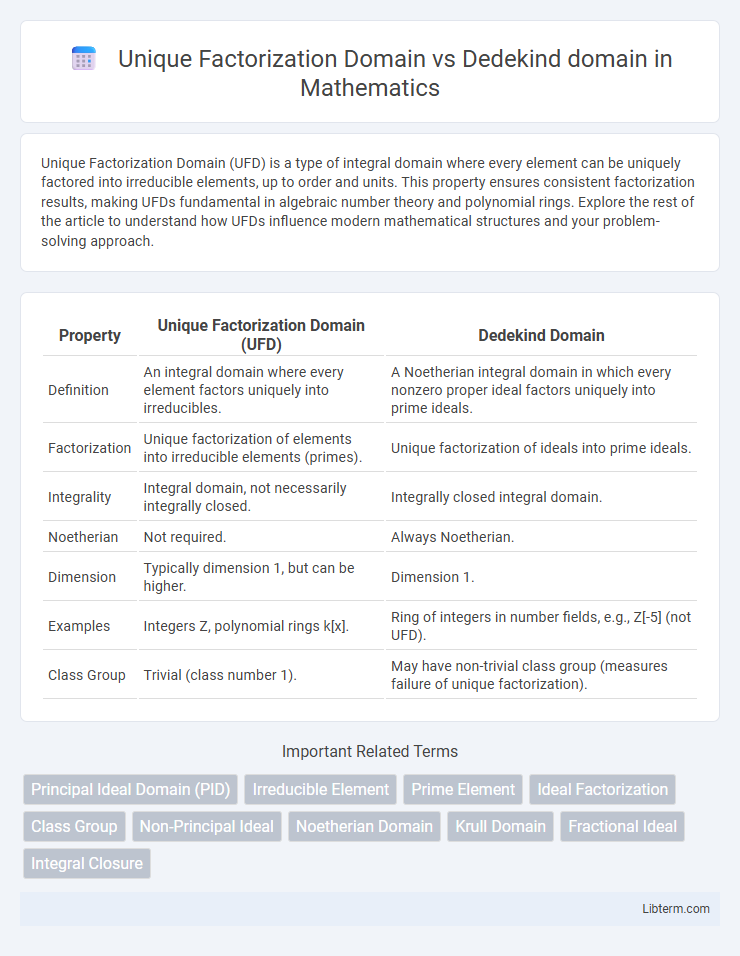
| Property | Unique Factorization Domain (UFD) | Dedekind Domain |
|---|---|---|
| Definition | An integral domain where every element factors uniquely into irreducibles. | A Noetherian integral domain in which every nonzero proper ideal factors uniquely into prime ideals. |
| Factorization | Unique factorization of elements into irreducible elements (primes). | Unique factorization of ideals into prime ideals. |
| Integrality | Integral domain, not necessarily integrally closed. | Integrally closed integral domain. |
| Noetherian | Not required. | Always Noetherian. |
| Dimension | Typically dimension 1, but can be higher. | Dimension 1. |
| Examples | Integers Z, polynomial rings k[x]. | Ring of integers in number fields, e.g., Z[-5] (not UFD). |
| Class Group | Trivial (class number 1). | May have non-trivial class group (measures failure of unique factorization). |
Introduction to Unique Factorization Domains
Unique Factorization Domains (UFDs) are integral domains where every nonzero, nonunit element can be written uniquely as a product of irreducible elements, up to order and units. This property generalizes the fundamental theorem of arithmetic from integers to more abstract rings, enabling a clear structure in factorization. Unlike Dedekind domains, which may lack unique factorization of elements but ensure unique factorization of ideals, UFDs emphasize element-level factorization uniqueness.
Key Properties of UFDs
Unique Factorization Domains (UFDs) are integral domains where every nonzero element can be uniquely factored into irreducible elements, mirroring the fundamental theorem of arithmetic. UFDs possess the ascending chain condition on principal ideals and are integrally closed, ensuring no further factorization ambiguities occur. Unlike Dedekind domains, which generalize unique factorization by prime ideals, UFDs guarantee element-level unique factorization, making factorization straightforward and explicitly describable.
Introduction to Dedekind Domains
Dedekind domains generalize Unique Factorization Domains (UFDs) by allowing unique factorization of ideals into prime ideals instead of elements, addressing factorization failures in rings of algebraic integers. These domains are integral domains that are Noetherian, integrally closed, and have Krull dimension one, ensuring well-behaved ideal structure. Understanding Dedekind domains is crucial for algebraic number theory, as they provide a natural framework for studying prime ideal decomposition and class groups.
Essential Properties of Dedekind Domains
Dedekind domains are integral domains characterized by the property that every nonzero proper ideal factors uniquely into a product of prime ideals, distinguishing them from Unique Factorization Domains where elements factor uniquely into irreducibles. Essential properties of Dedekind domains include being Noetherian, integrally closed in their field of fractions, and having Krull dimension one. These features enable Dedekind domains to generalize unique factorization beyond element factorization to ideal factorization, crucial in algebraic number theory and algebraic geometry.
Differences Between UFDs and Dedekind Domains
Unique Factorization Domains (UFDs) guarantee that every non-zero, non-unit element can be uniquely factored into irreducible elements, while Dedekind domains ensure unique factorization of ideals into prime ideals instead of elements. UFDs are integrally closed integral domains where factorization properties hold at the element level, whereas Dedekind domains are more general, characteristically integral closures of Noetherian domains with dimension one, focusing on ideal factorization. Key differences lie in the scope of factorization: UFDs factor elements uniquely, Dedekind domains factor ideals uniquely, often useful in algebraic number theory.
Examples of Unique Factorization Domains
Examples of Unique Factorization Domains (UFDs) include the ring of integers \(\mathbb{Z}\), polynomial rings over a field such as \(\mathbb{K}[x]\), and more generally, any principal ideal domain (PID) like \(\mathbb{Z}[i]\), the Gaussian integers. Unlike Dedekind domains, which generalize unique factorization to ideals rather than elements, UFDs guarantee that every element can be uniquely factored into irreducible elements. The distinction is critical in algebraic number theory where rings of integers in number fields serve as classic Dedekind domains but may fail to be UFDs.
Examples of Dedekind Domains
Dedekind domains generalize Unique Factorization Domains (UFDs) by allowing unique factorization of ideals into prime ideals, even when element factorization fails. Classic examples of Dedekind domains include the ring of integers in number fields such as the Gaussian integers \(\mathbb{Z}[i]\) and rings of algebraic integers like \(\mathbb{Z}[\sqrt{-5}]\), which are not UFDs but maintain ideal factorization properties. These domains are integral in algebraic number theory due to their robust structure supporting ideal class groups and factorization into prime ideals.
When is a Dedekind Domain a UFD?
A Dedekind domain is a Unique Factorization Domain (UFD) if and only if it is a Principal Ideal Domain (PID), meaning every ideal is generated by a single element. This condition ensures the factorization of ideals into prime ideals corresponds directly to the unique factorization of elements into irreducibles. Therefore, characterizing Dedekind domains as UFDs hinges on their ideal class group being trivial, indicating all fractional ideals are principal.
Factorization of Ideals vs Elements
Unique Factorization Domains (UFDs) guarantee that every element can be uniquely expressed as a product of irreducible elements, emphasizing factorization at the element level. Dedekind domains may fail unique factorization for elements but ensure that every nonzero ideal factors uniquely into prime ideals, highlighting ideal factorization. This distinction underscores that UFDs prioritize element factorization, while Dedekind domains provide a unique ideal factorization framework useful in algebraic number theory.
Applications and Importance in Algebraic Number Theory
Unique Factorization Domains (UFDs) provide a framework where every element can be uniquely factored into irreducibles, facilitating explicit integer-like factorization crucial in solving Diophantine equations and simplifying ring structure analysis. Dedekind domains generalize UFDs by ensuring unique factorization of ideals rather than elements, playing a fundamental role in algebraic number theory by enabling the study of ideal class groups, prime ideal decomposition in number fields, and providing the structural foundation for advanced theorems such as class field theory. The distinction between UFDs and Dedekind domains underpins much of algebraic number theory's approach to generalizing prime factorization and understanding the arithmetic of algebraic integers.
Unique Factorization Domain Infographic
 libterm.com
libterm.com