A subset is a set containing some or all elements of another set, maintaining order and distinct membership. Understanding subsets is fundamental in fields like mathematics, computer science, and data analysis, as they help define relationships within collections. Explore the rest of the article to deepen your grasp of subsets and their practical applications.
Table of Comparison
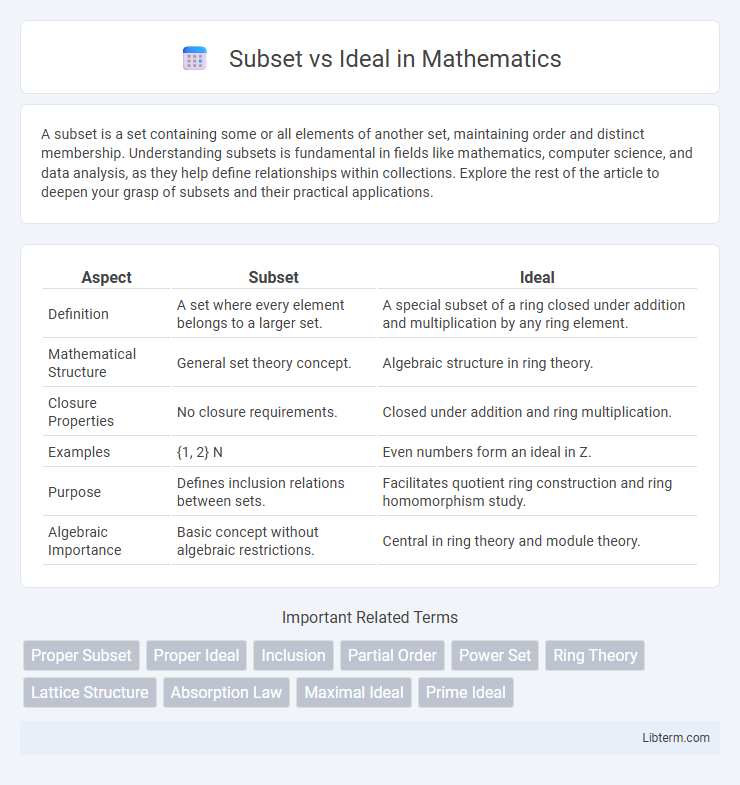
| Aspect | Subset | Ideal |
|---|---|---|
| Definition | A set where every element belongs to a larger set. | A special subset of a ring closed under addition and multiplication by any ring element. |
| Mathematical Structure | General set theory concept. | Algebraic structure in ring theory. |
| Closure Properties | No closure requirements. | Closed under addition and ring multiplication. |
| Examples | {1, 2} N | Even numbers form an ideal in Z. |
| Purpose | Defines inclusion relations between sets. | Facilitates quotient ring construction and ring homomorphism study. |
| Algebraic Importance | Basic concept without algebraic restrictions. | Central in ring theory and module theory. |
Understanding Subsets and Ideals: Definitions
A subset is a set where every element is contained within another set, defining a basic inclusion relationship in set theory. An ideal is a special subset within algebraic structures like rings, characterized by absorbing multiplication from elements of the ring and allowing the formation of quotient structures. Understanding subsets as foundational collections and ideals as algebraic structures with absorption properties helps distinguish their roles in mathematics.
Key Differences Between Subsets and Ideals
Subsets are any collections of elements contained within a larger set, whereas ideals are specific subsets in ring theory that absorb multiplication by ring elements and enable factor ring construction. Unlike general subsets, ideals must satisfy two conditions: they are additive subgroups and are closed under multiplication by any element in the ring. This makes ideals fundamental in algebraic structures for defining quotient rings, while subsets have no such algebraic closure requirements.
Properties of Subsets Explained
Subsets are defined as sets where every element of one set is contained within another, exhibiting properties such as reflexivity, transitivity, and antisymmetry that form the basis of the subset relation. Ideals, a special type of subset in ring theory, not only absorb multiplication by elements from the ring but also maintain the subset properties integral to algebraic structures. Understanding these subset properties aids in distinguishing ideals as subsets that are closed under ring operations and integral to constructing quotient rings.
Properties of Ideals in Algebraic Structures
Ideals in algebraic structures are special subsets that absorb multiplication by elements from the entire structure, making them crucial for constructing quotient structures and studying homomorphisms. Unlike general subsets, ideals must satisfy two main properties: they are additive subgroups and are closed under multiplication by any element of the larger algebraic structure. This allows ideals to serve as kernels of ring homomorphisms and facilitate the analysis of ring properties through factorization.
Subsets in Set Theory: Examples and Applications
Subsets in set theory are fundamental constructs where every element of one set is contained within another, exemplified by the set of even numbers being a subset of integers. These relationships facilitate operations in various mathematical fields, such as algebra and topology, by providing a structured way to analyze and categorize elements. Applications extend to computer science, particularly in database querying and logic programming, where understanding subset relations optimizes data retrieval and algorithm design.
Ideals in Ring Theory: Importance and Usage
Ideals in ring theory serve as fundamental building blocks for constructing quotient rings, enabling the study of ring homomorphisms and factorization properties. Unlike generic subsets, ideals must satisfy absorption under ring multiplication and addition closure, which ensures compatibility with ring operations and facilitates algebraic manipulation. Their significance extends to characterizing ring structures, simplifying complex problems, and underpinning key results like the isomorphism theorems and primary decomposition.
Criteria for Identifying Subsets vs Ideals
Subsets are identified primarily by the containment of all elements from one set within another, focusing on element inclusion and preserving membership relations. Ideals, a specialized type of subset in algebraic structures like rings or lattices, must satisfy additional absorption properties, such as being closed under addition and absorbing multiplication by elements from the entire structure. The key criterion distinguishing ideals from general subsets lies in these closure and absorption conditions, which ensure ideals serve as kernels for homomorphisms and facilitate quotient structure formation.
Subsets and Ideals: Real-World Applications
Subsets and ideals play crucial roles in abstract algebra and its applications across various scientific fields. Ideals, as specialized subsets of rings, facilitate the simplification of complex algebraic structures in cryptography, coding theory, and computational algebra. Understanding the difference between general subsets and ideals enhances data encryption techniques, error detection algorithms, and mathematical modeling in engineering disciplines.
Common Mistakes: Subset vs Ideal Confusion
Common mistakes in distinguishing subsets from ideals often arise from misunderstanding their algebraic properties; a subset may not necessarily satisfy the closedness conditions required of an ideal. Ideals must absorb multiplication by elements of the ring, a property not guaranteed by arbitrary subsets. Confusing these concepts leads to errors in proofs and ring theory applications, highlighting the importance of recognizing ideals as special subsets with additional structural constraints.
Summary Table: Subset vs Ideal Comparison
The Summary Table: Subset vs Ideal Comparison highlights the key differences in characteristics and applicability between subsets and ideals in algebraic structures. Subsets focus on inclusion and containment within a set, while ideals emphasize absorption under ring operations and enable quotient constructions. This comparison facilitates understanding of their roles in set theory and ring theory contexts, aiding in problem-solving and theoretical analysis.
Subset Infographic
 libterm.com
libterm.com