A direct functor is a fundamental concept in category theory that maps objects and morphisms from one category directly to another while preserving the structure. This means it respects composition and identity morphisms, ensuring that the relationships within the original category are maintained in the target category. Discover how understanding direct functors can enhance Your grasp of mathematical structures by reading the rest of the article.
Table of Comparison
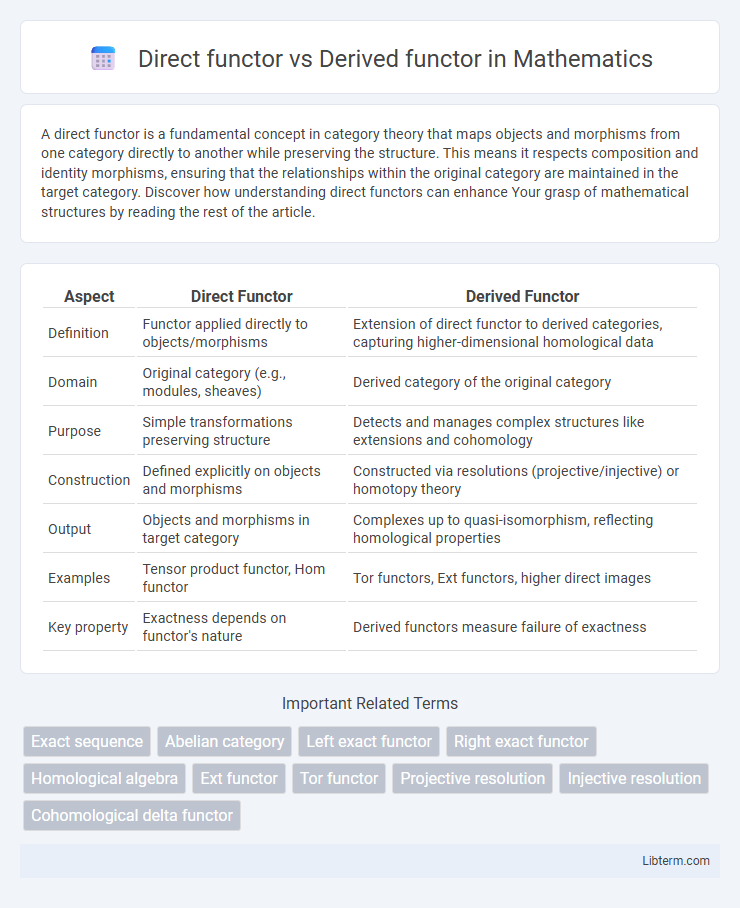
| Aspect | Direct Functor | Derived Functor |
|---|---|---|
| Definition | Functor applied directly to objects/morphisms | Extension of direct functor to derived categories, capturing higher-dimensional homological data |
| Domain | Original category (e.g., modules, sheaves) | Derived category of the original category |
| Purpose | Simple transformations preserving structure | Detects and manages complex structures like extensions and cohomology |
| Construction | Defined explicitly on objects and morphisms | Constructed via resolutions (projective/injective) or homotopy theory |
| Output | Objects and morphisms in target category | Complexes up to quasi-isomorphism, reflecting homological properties |
| Examples | Tensor product functor, Hom functor | Tor functors, Ext functors, higher direct images |
| Key property | Exactness depends on functor's nature | Derived functors measure failure of exactness |
Introduction to Functors in Category Theory
Direct functors map objects and morphisms between categories while preserving compositional structure, providing a foundation for categorical transformations. Derived functors extend direct functors by systematically measuring the failure of exactness, crucial in homological algebra and cohomology theories. Understanding direct and derived functors is essential for exploring complex interactions in abelian categories and triangulated categories.
Defining Direct Functors
Direct functors, also known as left exact functors, preserve finite limits and maintain the structure of morphisms between categories without introducing higher cohomological information. These functors operate by directly applying a mapping from one category to another, ensuring that kernels and finite inverse limits are preserved. In contrast, derived functors extend the concept of direct functors by capturing and measuring the failure of exactness through homological algebra techniques.
Understanding Derived Functors
Derived functors extend the concept of direct functors by measuring the failure of exactness in homological algebra, providing crucial tools for computing homology and cohomology groups. They arise from applying a functor to a projective or injective resolution, enabling the extraction of deeper structural information in categories like modules over a ring. Understanding derived functors is essential for analyzing extensions, Tor, and Ext functors, which reveal hidden layers of algebraic relationships beyond direct images.
Key Differences Between Direct and Derived Functors
Direct functors map objects and morphisms between categories without altering their intrinsic algebraic structures, preserving exact sequences only under specific conditions. Derived functors extend direct functors to homological contexts, capturing information about objects that direct functors fail to reflect by computing homology or cohomology groups. Key differences include their treatment of exactness: direct functors are exact or left/right exact by definition, whereas derived functors systematically handle non-exactness through chain complexes and resolutions, providing deeper insights into extensions and obstructions in homological algebra.
Applications of Direct Functors
Direct functors are extensively applied in algebraic topology and homological algebra to transform objects directly between categories while preserving structure, enabling straightforward computations of homology and cohomology groups. They facilitate exact functorial operations such as tensor products and hom functors, which are crucial in module theory and representation theory for constructing new modules or morphisms. In contrast to derived functors that address non-exactness, direct functors are preferred in settings where exactness properties simplify categorical analysis and computational efficiency.
Applications of Derived Functors
Derived functors extend the concept of direct functors by measuring the failure of exactness in homological algebra, crucial in computing cohomology groups in algebraic geometry and sheaf theory. They allow the extraction of deeper structural information from complex objects by analyzing higher homology or cohomology, essential in areas like Ext and Tor functors in module theory. Derived functors enable applications such as computing sheaf cohomology on complex varieties, resolving extension problems in category theory, and advancing spectral sequence constructions in homological algebra.
Examples Illustrating Direct vs. Derived Functors
Direct functors, such as the Hom functor \(\mathrm{Hom}_R(A, -)\), provide straightforward mappings between categories, while derived functors like Ext and Tor reveal deeper homological properties by measuring the failure of exactness. For example, the right derived functor of Hom, Ext\(^n_R(A, B)\), captures extension classes of modules, contrasting with the direct application of Hom that only reflects morphisms without extension information. Similarly, the Tor functor, a left derived functor of the tensor product, detects torsion phenomena that are invisible under the direct tensor product functor.
Importance in Homological Algebra
Direct functors preserve exact sequences, making them fundamental in the study of abelian categories and exactness properties. Derived functors extend direct functors to measure the failure of exactness, capturing deeper homological information such as extensions and higher Tor or Ext groups. The interplay between direct and derived functors is crucial in homological algebra for resolving objects and computing invariants that classify module and sheaf structures.
Common Misconceptions About Functors
Direct functors apply mappings straightforwardly between categories, preserving composition and identities, while derived functors extend this concept to homological algebra by computing objects like Ext and Tor through projective or injective resolutions. A common misconception is that derived functors simply "derive" from direct functors without additional structures; in reality, they require exact sequences and resolutions to capture deeper algebraic properties. Another frequent confusion lies in assuming all functors are exact, whereas direct functors may fail to preserve exactness, necessitating derived functors to measure this failure.
Conclusion: Choosing the Right Functor
Choosing the right functor depends on the context of the mathematical problem and the desired properties of the transformation, with direct functors offering simpler, straightforward mappings while derived functors handle complex structures by capturing deeper homological information. Derived functors are essential in homological algebra for extending direct functors to objects with intricate or non-exact sequences, capturing extensions, torsion, or cohomology groups that direct functors cannot reveal. Understanding the specific algebraic structures and exactness properties guides the selection between direct and derived functors to achieve precise and meaningful results in category theory and algebraic topology.
Direct functor Infographic
 libterm.com
libterm.com