An absolutely continuous measure is a measure that can be represented as an integral of a density function with respect to another measure, typically the Lebesgue measure. This concept is fundamental in measure theory and probability, where it ensures that no set of positive measure under the original measure is assigned zero measure by the absolutely continuous measure. Explore the full article to understand how absolutely continuous measures are applied in various mathematical and statistical contexts.
Table of Comparison
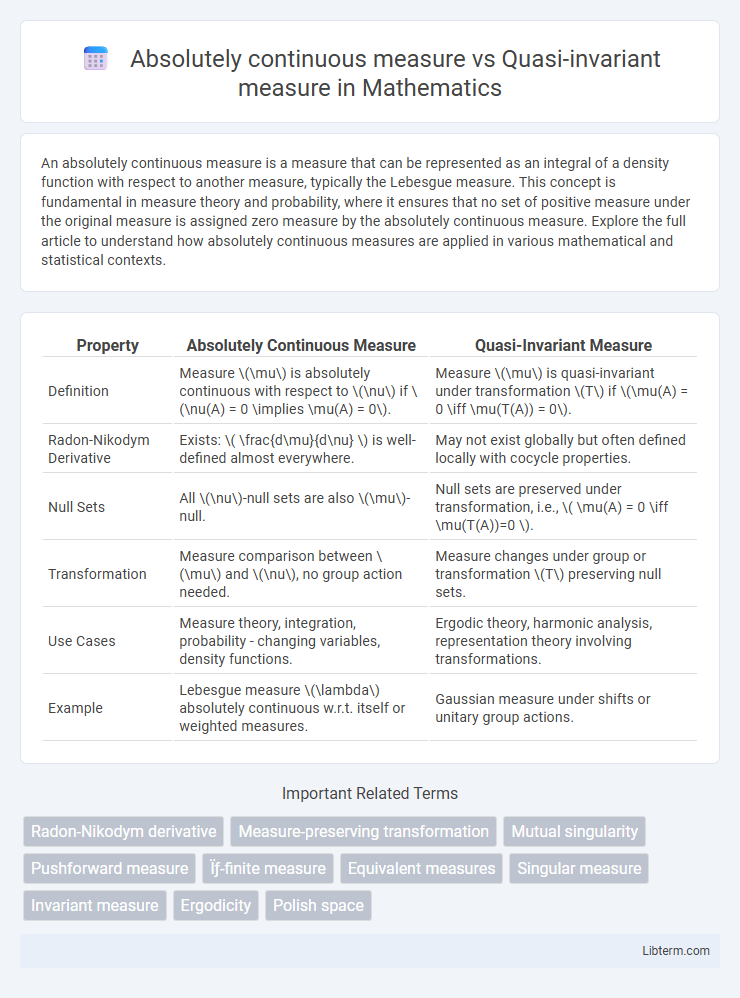
| Property | Absolutely Continuous Measure | Quasi-Invariant Measure |
|---|---|---|
| Definition | Measure \(\mu\) is absolutely continuous with respect to \(\nu\) if \(\nu(A) = 0 \implies \mu(A) = 0\). | Measure \(\mu\) is quasi-invariant under transformation \(T\) if \(\mu(A) = 0 \iff \mu(T(A)) = 0\). |
| Radon-Nikodym Derivative | Exists: \( \frac{d\mu}{d\nu} \) is well-defined almost everywhere. | May not exist globally but often defined locally with cocycle properties. |
| Null Sets | All \(\nu\)-null sets are also \(\mu\)-null. | Null sets are preserved under transformation, i.e., \( \mu(A) = 0 \iff \mu(T(A))=0 \). |
| Transformation | Measure comparison between \(\mu\) and \(\nu\), no group action needed. | Measure changes under group or transformation \(T\) preserving null sets. |
| Use Cases | Measure theory, integration, probability - changing variables, density functions. | Ergodic theory, harmonic analysis, representation theory involving transformations. |
| Example | Lebesgue measure \(\lambda\) absolutely continuous w.r.t. itself or weighted measures. | Gaussian measure under shifts or unitary group actions. |
Introduction to Measure Theory
Absolutely continuous measures arise when one measure is dominated by another, ensuring the first measure assigns zero to every set where the second measure is zero, crucial for Radon-Nikodym derivatives in measure theory. Quasi-invariant measures generalize this concept by allowing the measure to change under transformations, yet remain absolutely continuous with respect to its image measure, often explored in ergodic theory and group actions. Understanding their distinction is fundamental in analyzing how measures respond to mappings, especially within probability spaces and functional analysis frameworks.
Defining Absolutely Continuous Measures
Absolutely continuous measures are defined via the Radon-Nikodym theorem, where a measure m on a measurable space is absolutely continuous with respect to another measure n if for every measurable set A, n(A) = 0 implies m(A) = 0. This relationship allows the existence of a Radon-Nikodym derivative dm/dn, which serves as a density function expressing m in terms of n. In contrast, quasi-invariant measures permit sets of measure zero under n to have positive measure under m after transformations, lacking the strict null set preservation required for absolute continuity.
Understanding Quasi-invariant Measures
Quasi-invariant measures generalize absolutely continuous measures by allowing transformations that change the measure's support but preserve null sets. Unlike absolutely continuous measures, which require the Radon-Nikodym derivative to exist and be integrable, quasi-invariant measures maintain equivalence under group actions or measurable transformations up to a measurable density function. This property is fundamental in ergodic theory and harmonic analysis, where quasi-invariance ensures measure equivalence under dynamic systems or group symmetries.
Key Differences Between Absolutely Continuous and Quasi-invariant Measures
Absolutely continuous measures are defined such that if a set has zero measure under one measure, it also has zero measure under the other, ensuring a strict dominance relationship characterized by the Radon-Nikodym derivative. Quasi-invariant measures, however, do not require a zero measure set under one measure to be zero under the other but only that the null sets remain null after applying a group or transformation, preserving measure equivalence under a transformation group. The key difference lies in absolute continuity enforcing a stronger condition of measure domination, whereas quasi-invariance focuses on the preservation of null sets under transformations without necessarily having a Radon-Nikodym derivative relationship.
Radon-Nikodym Theorem and Its Role
The Radon-Nikodym theorem establishes that an absolutely continuous measure \(\nu\) with respect to a measure \(\mu\) admits a derivative \( \frac{d\nu}{d\mu} \), a measurable function that describes how \(\nu\) changes relative to \(\mu\). In contrast, quasi-invariant measures, often appearing in group actions, are not necessarily absolutely continuous but preserve measure class under transformations, lacking a straightforward Radon-Nikodym derivative. The theorem's critical role lies in enabling the decomposition of absolutely continuous measures for analysis and contrasting this with quasi-invariance highlights the measure-theoretic subtleties in ergodic theory and harmonic analysis.
Transformations and Their Impact on Measures
Absolutely continuous measures transform under measurable functions in a way that preserves null sets, meaning if a set has zero measure before transformation, its image also has zero measure, which ensures an explicit Radon-Nikodym derivative exists relating the transformed measure to the original. Quasi-invariant measures, by contrast, allow transformations that may alter null sets but preserve the class of null sets modulo measure zero, implying the measure is equivalent up to sets of zero measure but not necessarily absolutely continuous. This distinction critically affects ergodic theory and harmonic analysis, where absolutely continuous measures enable detailed density transformations, while quasi-invariant measures permit a broader class of transformations, facilitating studies of group actions and orbit structures.
Practical Examples of Absolutely Continuous Measures
Absolutely continuous measures commonly arise in probability theory, such as the normal distribution with its probability density function being absolutely continuous with respect to the Lebesgue measure. In signal processing, absolutely continuous measures model noise distributions where the Radon-Nikodym derivative represents the signal's density function. Quasi-invariant measures differ by allowing transformations that preserve measure class but not measure values, unlike absolutely continuous measures which require direct Radon-Nikodym derivatives for exact density representation.
Applications of Quasi-invariant Measures
Quasi-invariant measures play a crucial role in ergodic theory, representation theory, and probability on groups, enabling the study of measure-preserving transformations where the measure changes in an absolutely continuous way under group actions. They facilitate the construction of unitary representations of infinite-dimensional groups and support the analysis of orbit equivalence relations. Applications in statistical mechanics and dynamical systems leverage quasi-invariant measures to model systems with symmetries that are not strictly invariant but maintain absolute continuity of distributions.
Importance in Probability and Ergodic Theory
Absolutely continuous measures play a crucial role in probability theory by enabling Radon-Nikodym derivatives to express probability density functions relative to a reference measure, facilitating the rigorous formulation of likelihood and conditional expectations. Quasi-invariant measures are fundamental in ergodic theory, particularly in the study of dynamical systems, as they allow transformations that preserve measure classes without requiring strict invariance, thus enabling the analysis of long-term statistical behavior. The interplay between these measures underscores the ability to transfer properties through transformations and to analyze invariant or quasi-invariant structures vital for stochastic processes and ergodic decompositions.
Summary and Comparative Insights
Absolutely continuous measures possess a Radon-Nikodym derivative with respect to a reference measure, ensuring that null sets in the reference measure remain null in the absolutely continuous measure. Quasi-invariant measures allow transformations under which the measure remains equivalent, but not necessarily absolutely continuous, facilitating study of group actions and ergodic theory. Comparative analysis highlights absolute continuity's strict dominance relation versus quasi-invariance's flexibility in measure preservation under transformations.
Absolutely continuous measure Infographic
 libterm.com
libterm.com