Lattice structures offer remarkable strength-to-weight ratios, making them ideal for engineering and architectural applications. Their open framework allows for efficient material use while maintaining stability and durability. Discover how lattice designs can transform your projects by reading the full article.
Table of Comparison
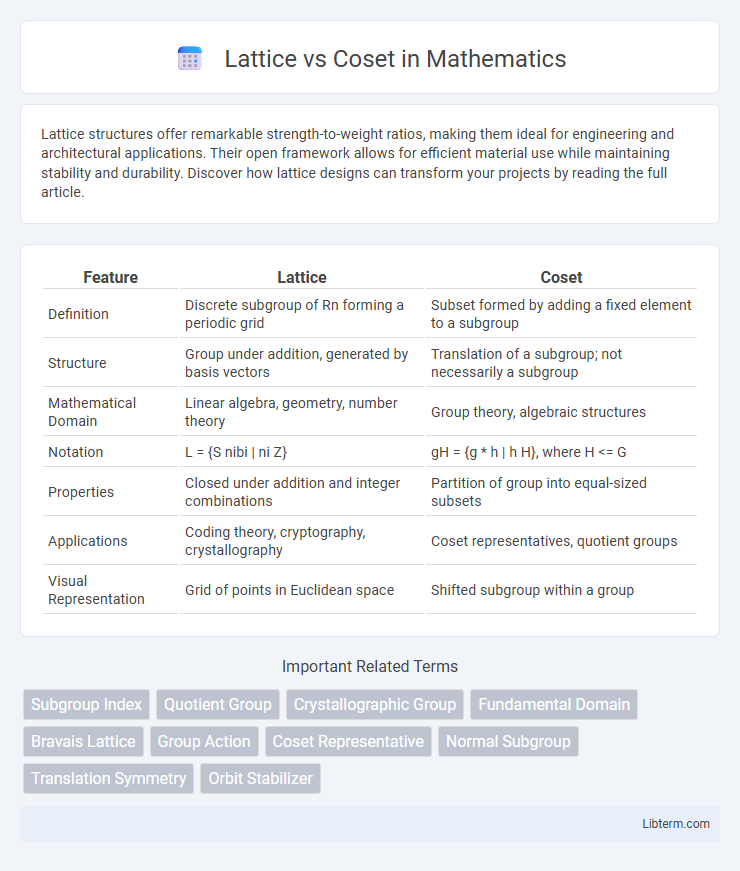
| Feature | Lattice | Coset |
|---|---|---|
| Definition | Discrete subgroup of Rn forming a periodic grid | Subset formed by adding a fixed element to a subgroup |
| Structure | Group under addition, generated by basis vectors | Translation of a subgroup; not necessarily a subgroup |
| Mathematical Domain | Linear algebra, geometry, number theory | Group theory, algebraic structures |
| Notation | L = {S nibi | ni Z} | gH = {g * h | h H}, where H <= G |
| Properties | Closed under addition and integer combinations | Partition of group into equal-sized subsets |
| Applications | Coding theory, cryptography, crystallography | Coset representatives, quotient groups |
| Visual Representation | Grid of points in Euclidean space | Shifted subgroup within a group |
Introduction to Lattice and Coset
Lattices are discrete, periodic arrangements of points in n-dimensional space generated by integer linear combinations of basis vectors, fundamental in cryptography and computational geometry. Cosets represent the partition of a group into equivalence classes formed by adding a fixed element to a subgroup, crucial for understanding group structure and symmetry. Both concepts provide foundational frameworks for solving problems in algebra, number theory, and coding theory.
Mathematical Definitions of Lattice and Coset
A lattice in mathematics is a discrete subgroup of \(\mathbb{R}^n\) formed by all integer linear combinations of a set of linearly independent vectors, serving as a fundamental structure in geometry and number theory. A coset, on the other hand, is defined as a subset formed by adding a fixed vector to every element of a lattice or subgroup, representing a translation of the original set. Understanding the distinction between lattices as regular grid-like structures and cosets as their shifted counterparts is crucial in areas such as group theory, cryptography, and coding theory.
Key Differences Between Lattice and Coset
Lattice and coset differ fundamentally in structure and algebraic properties; a lattice is a discrete subgroup of Euclidean space formed by integer linear combinations of basis vectors, while a coset represents a subset formed by adding a fixed element to a subgroup within a group. Lattices are used in cryptography and geometry for their regular grid patterns, whereas cosets provide insights into group partitioning and quotient group construction. The dimension and basis characterize lattices, whereas cosets depend on the subgroup and the chosen representative element defining the shift in group elements.
Lattice Structure: Properties and Examples
Lattice structure in mathematics is a partially ordered set in which every two elements have a unique supremum (join) and infimum (meet), defining a framework for algebraic and order-theoretic properties. Key properties include commutativity, associativity, absorption, and idempotency, which enable the construction of distributive and modular lattices fundamental in computer science and logic. Examples of lattice structures are the set of all subsets of a given set ordered by inclusion and the integer divisibility lattice, illustrating diverse applications in topology, abstract algebra, and data organization.
Coset Concept: Subgroups and Partitions
Coset concept in group theory involves partitioning a group into disjoint subsets called cosets, formed by multiplying a fixed subgroup by elements of the group. Each coset corresponds to an equivalence class under the relation defined by subgroup multiplication, ensuring that the group is divided into equal-sized partitions. This partitioning highlights the structure of subgroups within the group, facilitating an understanding of the group's composition and symmetries beyond lattice theory.
Algebraic Applications of Lattice and Coset
Lattices serve as discrete subgroup structures in vector spaces, fundamental for solving linear Diophantine equations, cryptography algorithms, and coding theory, where their geometric and algebraic properties facilitate basis reduction and integer programming. Cosets partition groups into equivalence classes, essential in group theory applications such as normal subgroup characterization, quotient group construction, and symmetry analysis in algebraic structures. Both lattices and cosets underpin advanced algebraic techniques in error-correcting codes, cryptanalysis, and group representation theory, enabling efficient problem-solving within abstract algebra and number theory.
Importance in Group Theory and Cryptography
Lattice and coset structures play crucial roles in group theory and cryptography, underpinning the complexity and security of many protocols. Lattices provide geometric frameworks for problems like the shortest vector problem, fundamental in constructing post-quantum cryptographic schemes such as Learning With Errors (LWE). Cosets facilitate the understanding of group partitions and quotient groups, essential in analyzing symmetries and designing efficient cryptographic algorithms based on group homomorphisms and subgroup structures.
Real-World Use Cases: Lattice vs Coset
Lattice-based cryptography is pivotal in securing communications for post-quantum cryptographic systems, widely adopted in secure messaging protocols and blockchain technologies due to its resistance to quantum attacks. Coset codes find significant application in error correction within wireless communication and data storage systems, enhancing reliability by efficiently correcting burst errors in noisy environments. Comparing both, lattice techniques excel in encryption and authentication frameworks, while coset methods are optimized for data integrity and transmission efficiency in real-world scenarios.
Comparison Table: Lattice versus Coset
Lattice theory revolves around a partially ordered set where every two elements have a unique supremum and infimum, emphasizing structure and order. Coset theory, rooted in group theory, examines subsets formed by multiplying a subgroup with a fixed group element, highlighting group partitioning. The comparison highlights distinct applications: lattices underpin data organization and logic systems, while cosets facilitate group factorization and symmetry analysis.
Conclusion: Choosing Between Lattice and Coset
Choosing between Lattice and Coset frameworks depends on the specific application requirements, with Lattice being ideal for lattice-based cryptography and post-quantum security, while Coset offers advantages in error-correcting codes and secure multiparty computation. Lattice structures provide strong resistance to classical and quantum attacks, making them suitable for encryption algorithms and digital signatures. Coset approaches excel in scenarios demanding efficient encoding and decoding with noise tolerance, such as network coding and privacy-preserving protocols.
Lattice Infographic
 libterm.com
libterm.com