Negative semidefinite matrices are symmetric matrices where all eigenvalues are less than or equal to zero, ensuring that for any vector x, the quadratic form xTAx is non-positive. These matrices play a crucial role in optimization problems and stability analysis in control theory. Dive deeper into this article to explore the properties, applications, and examples of negative semidefinite matrices.
Table of Comparison
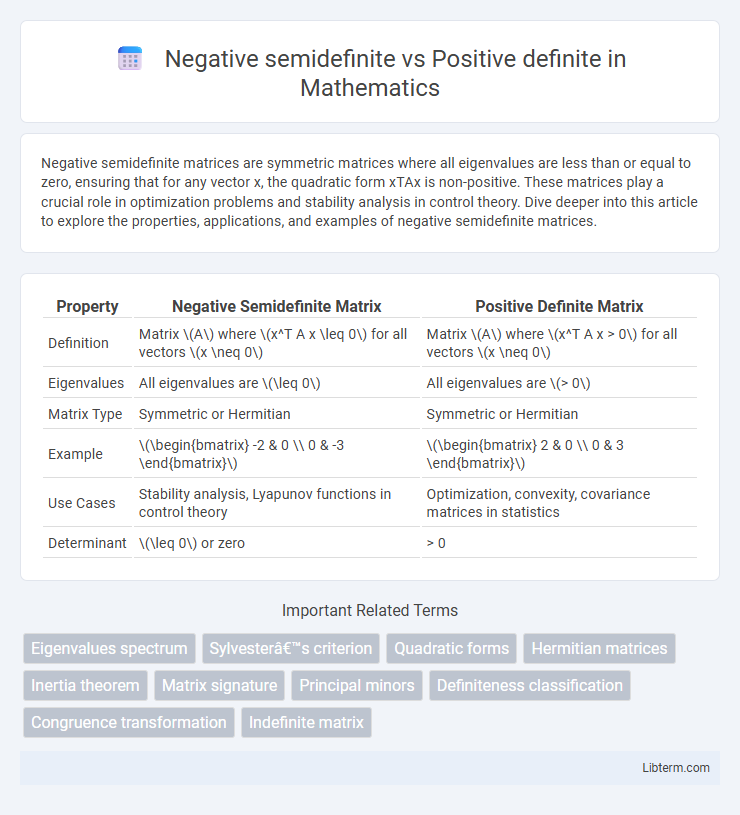
| Property | Negative Semidefinite Matrix | Positive Definite Matrix |
|---|---|---|
| Definition | Matrix \(A\) where \(x^T A x \leq 0\) for all vectors \(x \neq 0\) | Matrix \(A\) where \(x^T A x > 0\) for all vectors \(x \neq 0\) |
| Eigenvalues | All eigenvalues are \(\leq 0\) | All eigenvalues are \(> 0\) |
| Matrix Type | Symmetric or Hermitian | Symmetric or Hermitian |
| Example | \(\begin{bmatrix} -2 & 0 \\ 0 & -3 \end{bmatrix}\) | \(\begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix}\) |
| Use Cases | Stability analysis, Lyapunov functions in control theory | Optimization, convexity, covariance matrices in statistics |
| Determinant | \(\leq 0\) or zero | > 0 |
Understanding Definiteness: A Quick Overview
Positive definite matrices have strictly positive eigenvalues, ensuring all quadratic forms xTAx are greater than zero for any nonzero vector x, which implies stability and convexity in optimization problems. Negative semidefinite matrices feature eigenvalues that are less than or equal to zero, producing quadratic forms that are less than or equal to zero but can be zero for some nonzero vectors, often representing concave functions or stability boundaries. Understanding definiteness involves analyzing eigenvalue distributions and matrix behavior in quadratic forms to distinguish between guarantees of positivity, negativity, or borderline cases in system dynamics and optimization contexts.
What Does Positive Definite Mean?
Positive definite refers to a matrix whose quadratic form produces strictly positive values for all non-zero vectors, ensuring all its eigenvalues are positive. This property guarantees stability and invertibility in various applications such as optimization, statistics, and physics. Unlike negative semidefinite matrices, which yield non-positive quadratic forms, positive definite matrices indicate a strictly convex structure in mathematical models.
Defining Negative Semidefinite Matrices
Negative semidefinite matrices are defined as symmetric matrices whose eigenvalues are all less than or equal to zero, ensuring that for any nonzero vector \(x\), the quadratic form \(x^T A x \leq 0\). In contrast, positive definite matrices have strictly positive eigenvalues, making \(x^T A x > 0\) for any nonzero \(x\). Understanding the eigenvalue spectrum is crucial for distinguishing negative semidefinite matrices from positive definite ones.
Mathematical Criteria for Each Type
Negative semidefinite matrices have all eigenvalues less than or equal to zero, ensuring that for any vector \( x \), the quadratic form \( x^T A x \leq 0 \). Positive definite matrices require all eigenvalues to be strictly greater than zero, which guarantees \( x^T A x > 0 \) for all nonzero vectors \( x \). The principal minor test states that positive definiteness demands all leading principal minors be positive, while negative semidefiniteness requires them to be non-positive or alternate in sign depending on the matrix order.
Common Examples and Applications
Positive definite matrices frequently arise in optimization problems, such as Hessian matrices in convex functions ensuring local minima, and covariance matrices in statistics representing variance. Negative semidefinite matrices commonly appear in stability analysis, for example in Lyapunov functions demonstrating system stability, and in quadratic forms describing concave functions. Applications of positive definite matrices extend to machine learning algorithms like support vector machines, while negative semidefinite matrices are crucial in control theory for assessing system damping and energy dissipation.
Key Differences: Negative Semidefinite vs Positive Definite
Negative semidefinite matrices have all eigenvalues less than or equal to zero, indicating that quadratic forms produce non-positive values, while positive definite matrices possess strictly positive eigenvalues, ensuring positive quadratic forms. In optimization and stability analysis, positive definite matrices guarantee strict convexity and unique minima, whereas negative semidefinite matrices indicate concavity or flat regions without unique minima. The key difference lies in eigenvalue sign constraints and their implications for the behavior of associated quadratic forms and system stability.
Role in Optimization and Quadratic Forms
Positive definite matrices guarantee strictly convex quadratic forms, ensuring unique global minima in optimization problems and stable convergence in algorithms like gradient descent. Negative semidefinite matrices correspond to concave quadratic forms, which often represent maximization problems or constraints enforcing upper bounds in optimization frameworks. The definiteness property directly affects the Hessian matrix's behavior, influencing solution feasibility and optimality conditions in nonlinear programming.
Eigenvalues: The Telltale Signs
Positive definite matrices have strictly positive eigenvalues, indicating that all quadratic forms produce positive values except at the zero vector. Negative semidefinite matrices possess eigenvalues that are zero or negative, which means their associated quadratic forms are non-positive for any vector. Eigenvalue analysis offers a clear criterion for distinguishing matrix definiteness, with strictly positive eigenvalues confirming positive definiteness and non-positive eigenvalues indicating negative semidefiniteness.
Visualizing Matrix Definiteness
Visualizing matrix definiteness involves interpreting eigenvalue distributions and their impact on quadratic forms, where positive definite matrices exhibit strictly positive eigenvalues indicating convex surfaces, while negative semidefinite matrices possess non-positive eigenvalues leading to concave or flat regions. Heatmaps and contour plots of quadratic forms provide intuitive graphical representations, contrasting upward curvatures for positive definite matrices against downward or level curvatures for negative semidefinite ones. Eigenvalue spectra plots further clarify definiteness by highlighting zero or negative eigenvalues corresponding to matrix semidefiniteness compared to the strictly positive spectrum of positive definite matrices.
Practical Implications in Real-World Problems
Negative semidefinite matrices have eigenvalues less than or equal to zero, which typically indicate concave functions in optimization problems, often used in stability analysis and risk assessment. Positive definite matrices possess strictly positive eigenvalues, ensuring convexity and uniqueness of solutions, crucial for reliable convergence in machine learning algorithms and control systems. Understanding these properties aids in selecting appropriate models for portfolio optimization, structural engineering, and numerical simulations where system behavior prediction and solution stability are paramount.
Negative semidefinite Infographic
 libterm.com
libterm.com