Compatible devices and software ensure seamless integration and optimal performance across various platforms, enhancing user experience and productivity. Understanding compatibility requirements helps you avoid technical issues and maximize the benefits of your technology investments. Explore the article to discover key tips for ensuring compatibility in your digital environment.
Table of Comparison
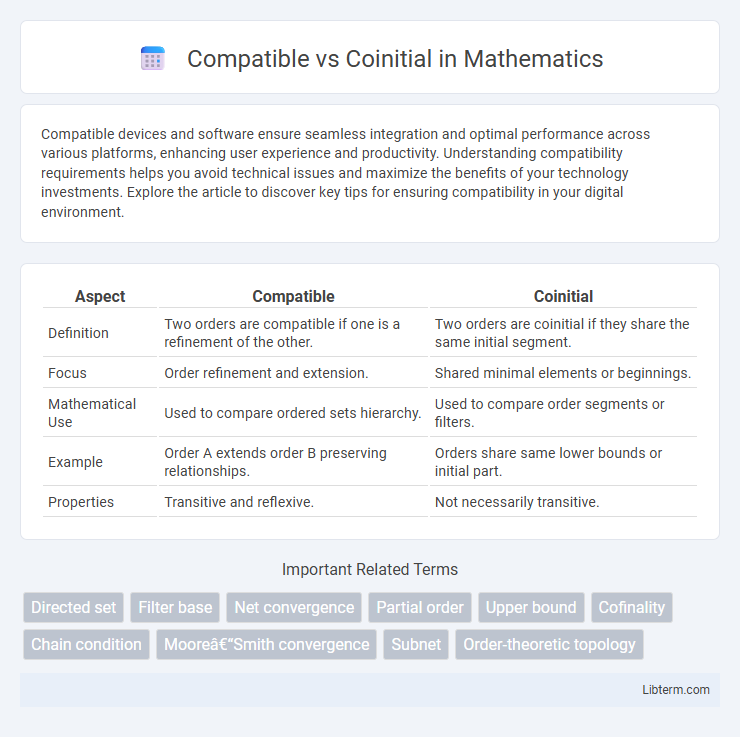
| Aspect | Compatible | Coinitial |
|---|---|---|
| Definition | Two orders are compatible if one is a refinement of the other. | Two orders are coinitial if they share the same initial segment. |
| Focus | Order refinement and extension. | Shared minimal elements or beginnings. |
| Mathematical Use | Used to compare ordered sets hierarchy. | Used to compare order segments or filters. |
| Example | Order A extends order B preserving relationships. | Orders share same lower bounds or initial part. |
| Properties | Transitive and reflexive. | Not necessarily transitive. |
Introduction to Compatible vs Coinitial
Compatible and coinitial relations are fundamental concepts in order theory, describing how elements within a partially ordered set (poset) interact. Two elements are compatible if they have a common upper bound, indicating a degree of coherence within the poset structure. Coinitial elements share a common lower bound, reflecting a foundational similarity in their positional hierarchy.
Defining Compatibility in Mathematical Structures
Compatibility in mathematical structures refers to the harmonious interaction between multiple structures imposed on the same set, ensuring they coexist without conflict. Coinitiality, a related but distinct concept, describes a scenario where directed systems share a common initial segment or element, facilitating comparison or unification. Defining compatibility involves verifying that operations, relations, or orders on the structures preserve essential properties when combined, such as ensuring that two topologies on a set are compatible if their intersection yields a topology.
Understanding Coinitiality: Key Concepts
Coinitiality in topology refers to two subsets that share the same initial elements or starting points within a given structure, reflecting a strong form of equivalence in their base behaviors. Understanding coinitial sets involves analyzing how their order-theoretic properties align, particularly in directed or ordered sets where coinitial subsets intersect at significant minimal elements. This concept is crucial in fields like domain theory and set theory, where coinitiality determines convergence and limits within ordered frameworks.
Differences Between Compatible and Coinitial Relations
Compatible relations occur when two elements or structures can coexist without conflict, ensuring seamless interaction or integration within a system. Coinitial relations specifically refer to elements sharing the same starting point or origin, often used in contexts like ordered sets or filters in mathematics and computer science. The key difference lies in compatibility addressing harmonious coexistence, whereas coinitiality emphasizes a common initial position or baseline within a structured framework.
Applications of Compatible Relations
Compatible relations play a crucial role in algebraic structures, ensuring that operations preserve equivalence relations, which is essential in constructing quotient structures and simplifying complex systems. In computer science, compatible relations enable modular verification by allowing substitution of equivalent components without altering system behavior, crucial in formal methods and programming language semantics. Their application extends to data classification and clustering, where maintaining compatibility guarantees consistency within equivalence classes for accurate pattern recognition and machine learning models.
Applications of Coinitial Relations
Coinitial relations find critical applications in database theory and information retrieval systems where aligning or synchronizing timestamps or event sequences is essential. These relations enable efficient querying and indexing by ensuring that two sequences share the same initial elements, facilitating temporal data analysis and event correlation. Coinitial relations also enhance concurrency control in distributed computing by maintaining consistent starting states across parallel processes.
Examples: Compatible vs Coinitial in Set Theory
Compatible sets often overlap or share common elements, as seen in the example where sets A = {1, 2, 3} and B = {2, 3, 4} are compatible because their intersection {2, 3} is non-empty. Coinitial sets, exemplified by subsets of the real numbers such as E = (1, ) and F = (2, ), are characterized by the property that every element of one set has a greater or equal element in the other, making them cofinal in the same order. In set theory, compatibility emphasizes intersection and element sharing, whereas coinitiality focuses on order relations and shared lower bounds within a partially ordered set.
Significance in Order Theory and Category Theory
Compatible and coinitial relations hold significant roles in order theory and category theory by structuring how elements and morphisms interact within posets and categories. Compatible relations ensure consistency and preserve order properties when combining or comparing elements, critical for defining continuous lattices and directed sets. Coinitial sets characterize minimal elements or subsets intersecting all nonempty lower sets, aiding in defining initial objects and understanding foundational constructions in categorical limits and colimits.
Potential Overlaps and Common Confusions
Compatible and coinitial often cause confusion due to their overlapping applications in mathematics and logic. Compatible typically refers to elements or operations that can coexist without conflict, ensuring consistency within a system, while coinitial describes objects or sequences sharing a common starting point or initial segment. Understanding their distinct roles is crucial, as compatibility emphasizes harmonious interaction, whereas coinitiality focuses on shared origins or alignment in initial structure.
Summary: Choosing Between Compatible and Coinitial
Choosing between compatible and coinitial structures depends on the specific categorical context and desired outcomes in mathematical or logical frameworks. Compatible morphisms preserve structural alignment, allowing for coherent interaction within defined systems, whereas coinitial morphisms emphasize initial or minimal properties relevant to limit and colimit constructions. Understanding the functional goals--such as ensuring commutativity or optimizing initial object behavior--guides the selection of compatible versus coinitial morphisms in category theory applications.
Compatible Infographic
 libterm.com
libterm.com