Mastering complex concepts requires breaking down intricate ideas into manageable parts to enhance understanding and retention. By developing structured approaches and employing critical thinking strategies, you can navigate complexity more effectively. Explore the rest of the article to discover practical techniques that will empower your learning journey.
Table of Comparison
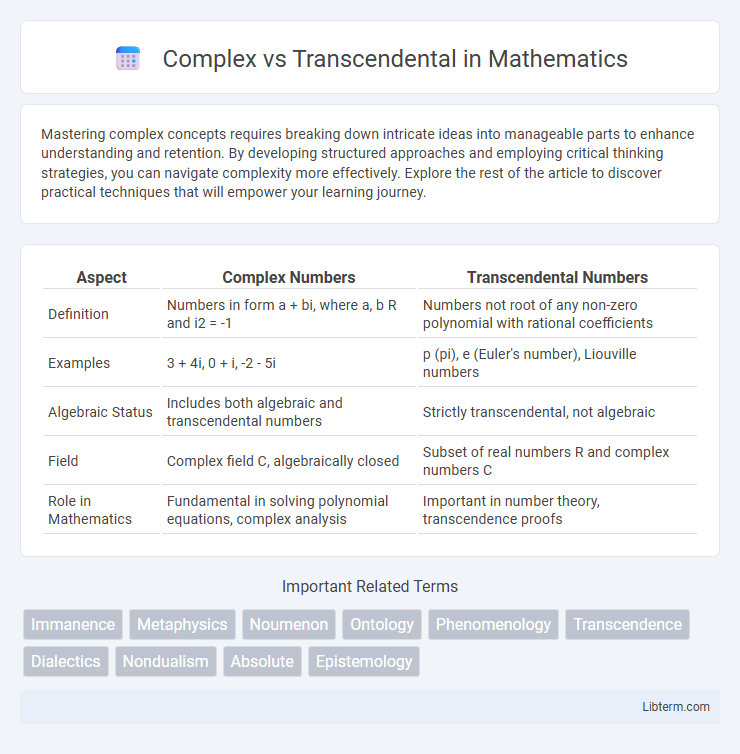
| Aspect | Complex Numbers | Transcendental Numbers |
|---|---|---|
| Definition | Numbers in form a + bi, where a, b R and i2 = -1 | Numbers not root of any non-zero polynomial with rational coefficients |
| Examples | 3 + 4i, 0 + i, -2 - 5i | p (pi), e (Euler's number), Liouville numbers |
| Algebraic Status | Includes both algebraic and transcendental numbers | Strictly transcendental, not algebraic |
| Field | Complex field C, algebraically closed | Subset of real numbers R and complex numbers C |
| Role in Mathematics | Fundamental in solving polynomial equations, complex analysis | Important in number theory, transcendence proofs |
Understanding Complex Numbers: A Brief Overview
Complex numbers consist of a real part and an imaginary part, expressed as a + bi, where "i" represents the square root of -1. They extend the real number system and enable solutions to equations that have no real roots, such as x2 + 1 = 0. Transcendental numbers, like p and e, are real or complex numbers that are not roots of any non-zero polynomial equation with rational coefficients, highlighting a fundamental difference in classification within number theory.
The Essence of Transcendental Numbers
Transcendental numbers, unlike complex numbers that include all real and imaginary numbers, cannot be expressed as solutions to any non-zero polynomial equation with rational coefficients. The essence of transcendental numbers lies in their non-algebraic nature, making constants like p and e fundamental in understanding mathematical irrationality and complexity. This distinction highlights the profound depth in number theory where transcendental numbers transcend algebraic constraints inherent in complex numbers.
Key Differences: Complex vs. Transcendental Numbers
Complex numbers include all numbers in the form a + bi, where a and b are real numbers and i is the imaginary unit satisfying i2 = -1, encompassing real and imaginary numbers. Transcendental numbers, a subset of real or complex numbers, are not roots of any non-zero polynomial equation with rational coefficients, examples being p and e. The key difference is that all transcendental numbers are complex numbers but not all complex numbers are transcendental, as many complex numbers are algebraic and satisfy polynomial equations.
Historical Milestones in the Study of Both Types
The study of complex numbers began in the 16th century with solutions to cubic equations, notably by mathematicians like Gerolamo Cardano and Rafael Bombelli, who laid the foundation for complex analysis. Transcendental numbers were first identified in the 19th century, with Joseph Liouville proving their existence and Charles Hermite demonstrating the transcendence of e in 1873, followed by Ferdinand von Lindemann proving p's transcendence in 1882. These milestones have profoundly advanced mathematical understanding, distinguishing algebraic complex numbers from transcendental ones beyond algebraic roots.
Famous Examples: Complex and Transcendental Numbers
Famous examples of complex numbers include \(3 + 4i\) and Euler's identity \(e^{i\pi} + 1 = 0\), which combine real and imaginary parts. Transcendental numbers like \(\pi\) and \(e\) are non-algebraic, meaning they cannot be roots of any non-zero polynomial with rational coefficients. While every transcendental number is complex, not all complex numbers are transcendental since many complex numbers are algebraic or purely imaginary.
Applications in Mathematics and Science
Complex numbers, expressed as a + bi where i is the imaginary unit, are fundamental in fields like engineering, quantum physics, and signal processing for solving equations that real numbers cannot. Transcendental numbers, such as p and e, arise in calculus, number theory, and chaos theory, representing values that are not roots of any algebraic equation with rational coefficients. The distinct roles of complex and transcendental numbers enable advanced mathematical modeling, numerical analysis, and the description of natural phenomena beyond polynomial constructs.
The Role of Algebraic Numbers in Contrast
Algebraic numbers play a crucial role in distinguishing complex numbers from transcendental numbers, as the former encompasses all roots of polynomial equations with rational coefficients, while transcendental numbers lie beyond any such algebraic solutions. Complex numbers include not only algebraic numbers but also transcendental numbers like p and e, which cannot be expressed as roots of polynomial equations. Understanding the properties of algebraic numbers helps clarify the structural boundaries within the complex number system, highlighting the unique nature of transcendental numbers in number theory.
Visualizing Complex and Transcendental Concepts
Visualizing complex concepts often involves using multi-dimensional graphs or fractal patterns to represent intricate relationships within complex numbers and their behaviors. Transcendental concepts, such as transcendental functions and numbers, are depicted through dynamic plots showing non-algebraic growth and oscillations, which cannot be expressed as roots of polynomial equations. Tools like 3D parametric models and computer-generated imagery enhance understanding by illustrating abstract transcendental phenomena beyond traditional algebraic visualizations.
Challenges in Identifying Transcendental Numbers
Identifying transcendental numbers presents significant challenges due to their non-algebraic nature, which means they cannot be roots of any non-zero polynomial equation with rational coefficients, unlike complex numbers that include both algebraic and transcendental types. The difficulty arises from the need to prove that no polynomial relation exists, a task that often involves intricate theorems from transcendental number theory, such as the Lindemann-Weierstrass theorem. This complexity limits the number of known transcendental numbers despite their abundance in the real and complex number sets.
The Future of Research: Unsolved Problems and New Frontiers
Research into complex numbers and transcendental numbers continues to push mathematical boundaries, revealing unsolved problems like the Riemann Hypothesis and the distribution of transcendental values of complex functions. Exploring these frontiers enhances understanding of number theory, complex analysis, and algebraic geometry, with implications for cryptography and quantum computing. Advances in computational methods and interdisciplinary approaches drive future discoveries in these challenging mathematical domains.
Complex Infographic
 libterm.com
libterm.com