Lie algebra is a fundamental structure in mathematics used to study geometric and algebraic properties through non-associative algebras characterized by the Lie bracket. It plays a crucial role in understanding symmetry, differential equations, and theoretical physics, especially in quantum mechanics and particle physics. Discover how Lie algebra can deepen your grasp of these complex concepts by exploring the rest of this article.
Table of Comparison
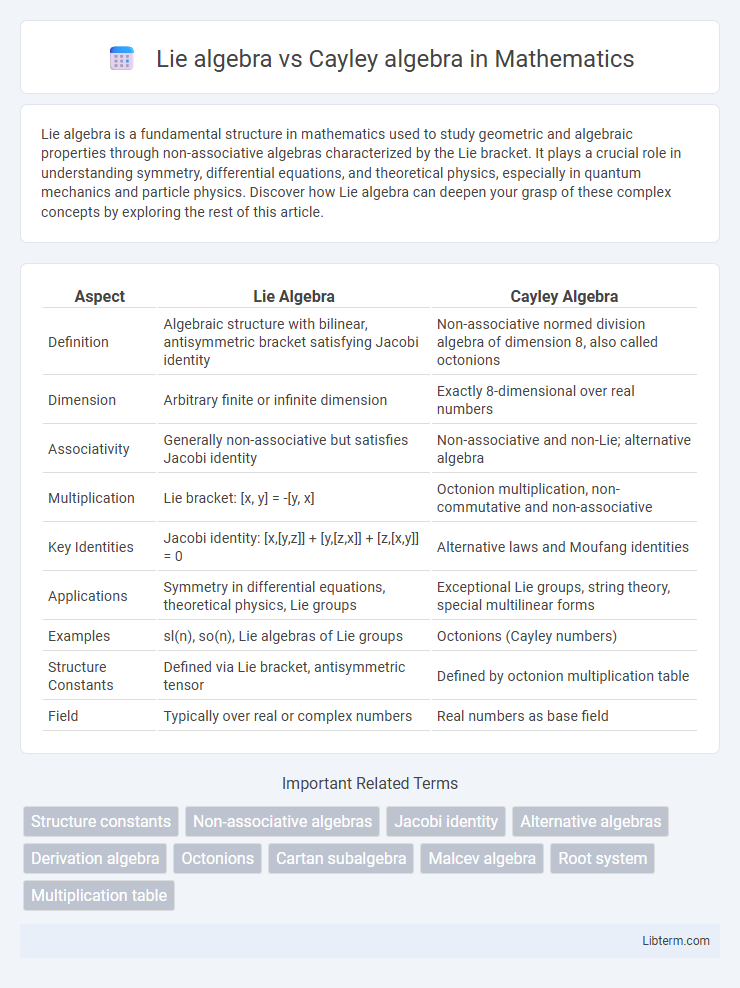
| Aspect | Lie Algebra | Cayley Algebra |
|---|---|---|
| Definition | Algebraic structure with bilinear, antisymmetric bracket satisfying Jacobi identity | Non-associative normed division algebra of dimension 8, also called octonions |
| Dimension | Arbitrary finite or infinite dimension | Exactly 8-dimensional over real numbers |
| Associativity | Generally non-associative but satisfies Jacobi identity | Non-associative and non-Lie; alternative algebra |
| Multiplication | Lie bracket: [x, y] = -[y, x] | Octonion multiplication, non-commutative and non-associative |
| Key Identities | Jacobi identity: [x,[y,z]] + [y,[z,x]] + [z,[x,y]] = 0 | Alternative laws and Moufang identities |
| Applications | Symmetry in differential equations, theoretical physics, Lie groups | Exceptional Lie groups, string theory, special multilinear forms |
| Examples | sl(n), so(n), Lie algebras of Lie groups | Octonions (Cayley numbers) |
| Structure Constants | Defined via Lie bracket, antisymmetric tensor | Defined by octonion multiplication table |
| Field | Typically over real or complex numbers | Real numbers as base field |
Introduction to Lie Algebra and Cayley Algebra
Lie algebra is a mathematical structure characterized by a vector space equipped with a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, playing a fundamental role in the study of continuous symmetries and differential equations. Cayley algebra, also known as the octonion algebra, is an example of a non-associative algebra over the real numbers, extending quaternions and characterized by an eight-dimensional normed division algebra with alternative multiplication. Both Lie algebras and Cayley algebras are crucial in advanced algebraic research, with Lie algebras focusing on infinitesimal transformations and Cayley algebras providing examples of non-associative division algebras.
Historical Background and Development
Lie algebra emerged in the late 19th century through Sophus Lie's work on continuous transformation groups, providing a foundational framework for studying symmetries and differential equations. Cayley algebra, or Cayley-Dickson construction, developed in the late 19th and early 20th centuries originated from Arthur Cayley's exploration of octonions, expanding complex numbers and quaternions into non-associative algebras. Both algebras played crucial roles in advancing modern algebra and theoretical physics by formalizing structures underlying symmetry and geometric transformations.
Fundamental Concepts of Lie Algebra
Lie algebra is a mathematical structure characterized by a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, which encodes the concept of infinitesimal transformations. Cayley algebra, also known as the octonion algebra, is a non-associative division algebra extending quaternions, lacking the Lie algebra's Jacobi identity property. Understanding Lie algebras involves studying their generators, structure constants, and representation theory, which underpin symmetry analysis in physics and geometry.
Key Principles of Cayley Algebra
Cayley algebra, also known as octonions, is a non-associative extension of quaternions characterized by its eight-dimensional composition and alternativity, distinguishing it from Lie algebras which are associative and satisfy the Jacobi identity. The key principles of Cayley algebra include the use of a normed division algebra structure with non-associative multiplication, the presence of a conjugation operation that preserves the norm, and the construction based on the Cayley-Dickson process. Unlike Lie algebras that model symmetry through commutation relations, Cayley algebras provide a framework for understanding exceptional structures in mathematics and theoretical physics, such as exceptional Lie groups and triality phenomena.
Structural Differences Between Lie and Cayley Algebras
Lie algebras are characterized by a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, enabling the study of infinitesimal symmetries and Lie group structures. Cayley algebras, also known as octonion algebras, are non-associative composition algebras with a multiplication operation that is neither associative nor commutative but alternative, featuring a norm preserving multiplication. Structurally, Lie algebras operate through commutator brackets emphasizing infinitesimal transformations, whereas Cayley algebras focus on normed division properties and alternative multiplication, resulting in fundamentally different algebraic identities and applications.
Algebraic Operations and Properties
Lie algebras are characterized by a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, which defines their algebraic structure and underpins their role in representing continuous symmetries. Cayley algebras, also known as octonions, are non-associative normed division algebras featuring a multiplicative operation that is alternative but not associative, extending quaternionic multiplication with seven imaginary units. While Lie algebra multiplication is strictly Lie bracket-based and linear, Cayley algebra operations involve non-associative product rules with properties like alternativity and norm composition, crucial for understanding exceptional algebraic structures.
Applications in Mathematics and Physics
Lie algebras are fundamental in representing continuous symmetries in mathematics and theoretical physics, particularly in quantum mechanics, particle physics, and the study of differential equations. Cayley algebras, or octonions, extend complex numbers and quaternions, playing a role in special structures within geometry, string theory, and exceptional Lie groups. Both algebras offer deep insights into symmetry, with Lie algebras underpinning gauge theory and Cayley algebras contributing to understanding triality and exceptional phenomena in higher-dimensional frameworks.
Representation Theory in Lie and Cayley Algebras
Lie algebra representation theory centers on linear actions on vector spaces, using modules to study algebraic structures via matrix Lie groups and Lie algebras, with classifications such as highest weight theory playing a crucial role. Cayley algebras, especially octonion algebras, exhibit non-associative properties that complicate their representation theory, often requiring alternative algebraic frameworks and exceptional Lie group connections like G2 to understand their modules. The interplay between Lie and Cayley algebras in representation theory hinges on the exceptional structures and decompositions that link octonions to symmetry groups and their representations.
Similarities and Distinctions Summarized
Lie algebras and Cayley algebras both play significant roles in abstract algebra, with Lie algebras focused on the study of algebraic structures related to Lie groups, characterized by antisymmetric bilinear brackets satisfying the Jacobi identity. Cayley algebras, or octonions, are non-associative normed division algebras notable for their alternative multiplication and lack of the Jacobi identity, contrasting with Lie algebras. Both share non-associativity, but Lie algebras emphasize linear operations and symmetry properties, while Cayley algebras extend beyond associativity to enable normed division and possess unique automorphism groups like G2.
Future Directions and Research Trends
Emerging research in Lie algebra emphasizes exploring infinite-dimensional cases and their applications in quantum computing and string theory, highlighting deeper symmetry structures in mathematical physics. Cayley algebra studies focus on non-associative algebra extensions and their role in exceptional Lie groups and octonions, aiming to unlock new geometric and topological insights. Future directions point toward integrating computational techniques and category theory to advance understanding of algebraic structures and their applications in theoretical physics and cryptography.
Lie algebra Infographic
 libterm.com
libterm.com