Planes revolutionize travel by enabling rapid transportation across vast distances, connecting continents and cultures efficiently. Advanced aerodynamics and powerful jet engines ensure safety and speed, making air travel accessible to millions worldwide. Explore the rest of this article to discover how planes impact your journeys and the future of aviation technology.
Table of Comparison
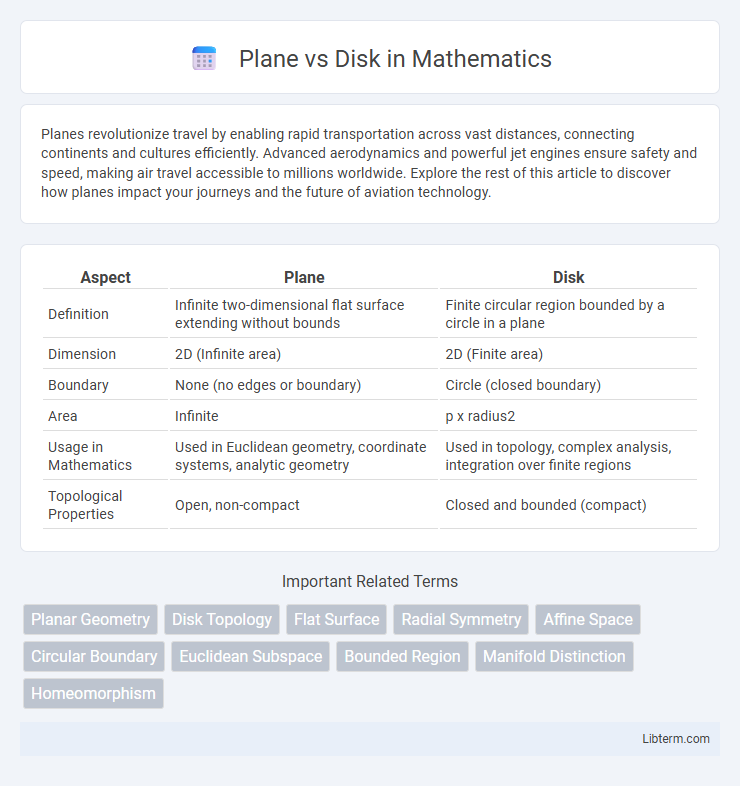
| Aspect | Plane | Disk |
|---|---|---|
| Definition | Infinite two-dimensional flat surface extending without bounds | Finite circular region bounded by a circle in a plane |
| Dimension | 2D (Infinite area) | 2D (Finite area) |
| Boundary | None (no edges or boundary) | Circle (closed boundary) |
| Area | Infinite | p x radius2 |
| Usage in Mathematics | Used in Euclidean geometry, coordinate systems, analytic geometry | Used in topology, complex analysis, integration over finite regions |
| Topological Properties | Open, non-compact | Closed and bounded (compact) |
Introduction: Understanding Plane vs. Disk
A plane is a flat, two-dimensional surface extending infinitely in all directions, characterized by length and width but no thickness. A disk is a specific region within a plane, defined as all points within a fixed radius from a central point, representing a bounded area. Understanding the distinction between the infinite nature of a plane and the finite, circular area of a disk is fundamental in geometry and spatial analysis.
Definitions: What is a Plane? What is a Disk?
A plane is a flat, two-dimensional surface extending infinitely in all directions with zero thickness, defined mathematically by a linear equation in three-dimensional space. A disk is a two-dimensional geometric figure consisting of all points within a fixed radius from a central point, representing a finite, bounded region lying on a plane. The primary distinction lies in the plane being infinite and unbounded, while the disk is a finite subset of the plane enclosed by a circular boundary.
Mathematical Properties: Plane vs. Disk
A plane is an infinite two-dimensional surface characterized by an unbounded set of points satisfying a linear equation in Euclidean space. A disk is a bounded subset of a plane defined as all points within a fixed radius from a central point, forming a closed, convex region. The plane has infinite area and no boundary, whereas the disk has finite area pr2 and a circular boundary of circumference 2pr.
Geometric Differences
Planes are flat, two-dimensional surfaces extending infinitely in all directions, defined by a linear equation in three-dimensional space. Disks are bounded, circular regions on a plane, with a finite radius and area, representing a subset of the plane. The primary geometric difference lies in the plane's unbounded nature versus the disk's limited boundary and measurable size.
Topological Comparison
A plane is a two-dimensional surface extending infinitely in all directions with zero curvature, while a disk is a bounded two-dimensional manifold homeomorphic to a closed unit ball in Euclidean space. Topologically, the disk is compact with a boundary homeomorphic to a circle, distinguishing it from the plane, which is non-compact and boundaryless. This fundamental difference makes the plane simply connected without boundary, whereas the disk has a well-defined boundary affecting its homotopy and homology groups.
Real-world Applications
Planes are extensively utilized in computational geometry for 3D modeling, architectural design, and robotics navigation, providing a foundational reference for object orientation and spatial calculations. Disks find real-world applications in computer graphics for texture mapping, in storage devices like hard disk drives for data retrieval, and in network topologies representing local area networks (LANs). Both geometric shapes serve crucial roles in engineering simulations, virtual reality environments, and geographic information systems (GIS) for accurate spatial representation and analysis.
Visual Representation: Plane and Disk
The visual representation of a plane is typically an infinite flat surface extending in all directions, often depicted as a parallelogram within a coordinate system to imply its endless nature. In contrast, a disk is a two-dimensional circular region bounded by a closed curve, usually shown as a filled circle or shaded area within a plane, emphasizing its finite area. The plane emphasizes unbounded continuity, while the disk highlights a specific, limited section of that plane.
Boundary Considerations
In geometry, a plane is an infinite flat surface without boundaries, while a disk is a finite region bounded by a circle. Boundary considerations are crucial when analyzing properties like perimeter, area, or topological features since a plane has no edges, but a disk has a clear closed boundary. This distinction affects integration limits, surface topology, and boundary conditions in mathematical and physical applications.
Advantages and Limitations
A plane offers the advantage of infinite extent, allowing for simplified calculations in geometry and computer graphics without boundary constraints, but it lacks realism when modeling finite objects. A disk provides a finite, circular boundary that better represents real-world objects with a clear limit, improving practicality in applications like collision detection and rendering. However, the limitation of a disk lies in its bounded nature, which can complicate mathematical operations that assume infinite surfaces.
Conclusion: Key Takeaways
Planes provide an infinite flat surface ideal for theoretical mathematics and computer graphics, while disks represent finite, round shapes essential in practical applications like storage media and mechanical components. Understanding the distinctions in geometry, boundary conditions, and dimensional constraints enables optimized use of each shape in design and analysis. Selecting between a plane or a disk hinges on the specific requirements of space, continuity, and application-driven limitations.
Plane Infographic
 libterm.com
libterm.com