The determinant is a fundamental concept in linear algebra, representing a scalar value that can be computed from the elements of a square matrix. It provides essential insights into the matrix's properties, such as invertibility and volume scaling in transformations. Explore the rest of this article to deepen your understanding of how determinants influence mathematical and real-world applications.
Table of Comparison
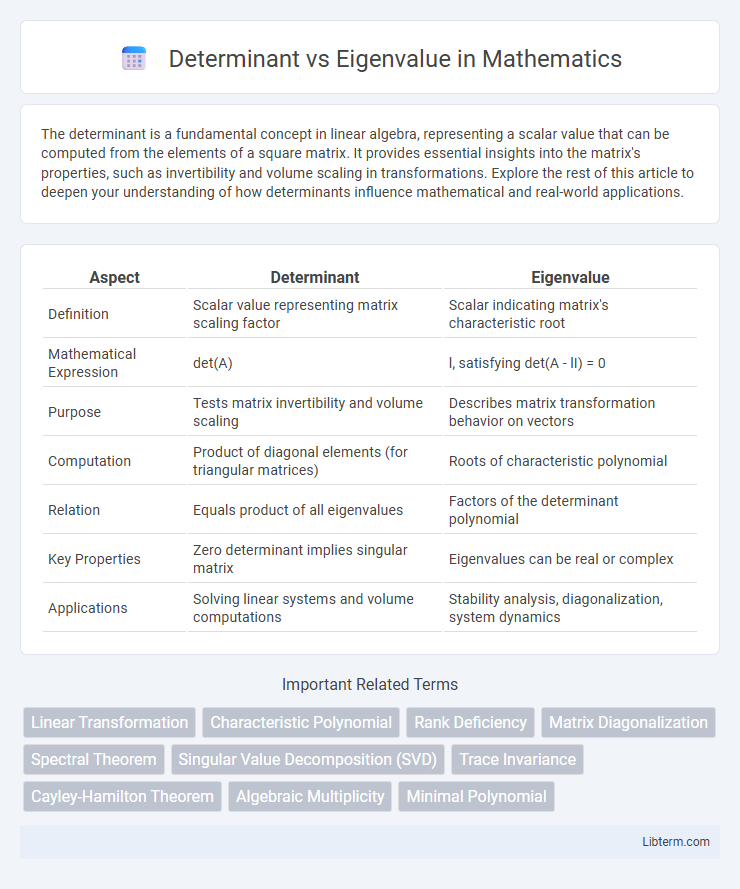
| Aspect | Determinant | Eigenvalue |
|---|---|---|
| Definition | Scalar value representing matrix scaling factor | Scalar indicating matrix's characteristic root |
| Mathematical Expression | det(A) | l, satisfying det(A - lI) = 0 |
| Purpose | Tests matrix invertibility and volume scaling | Describes matrix transformation behavior on vectors |
| Computation | Product of diagonal elements (for triangular matrices) | Roots of characteristic polynomial |
| Relation | Equals product of all eigenvalues | Factors of the determinant polynomial |
| Key Properties | Zero determinant implies singular matrix | Eigenvalues can be real or complex |
| Applications | Solving linear systems and volume computations | Stability analysis, diagonalization, system dynamics |
Introduction to Determinants and Eigenvalues
Determinants provide a scalar value representing the scaling factor of a linear transformation described by a square matrix, essential for assessing matrix invertibility and volume distortion. Eigenvalues denote specific scalars associated with a matrix that, when multiplied by an eigenvector, yield the same vector after transformation, highlighting intrinsic properties like stability and resonance in systems. Both determinants and eigenvalues play crucial roles in linear algebra, with determinants reflecting overall matrix behavior and eigenvalues revealing directional characteristics of transformations.
Definition of Determinant
The determinant is a scalar value derived from a square matrix that provides crucial information about the matrix's invertibility and the volume scaling factor of the linear transformation it represents. It is calculated through specific arithmetic on the matrix elements, reflecting properties such as singularity when the determinant equals zero. Eigenvalues, by contrast, are characteristic scalars associated with a matrix indicating the factors by which eigenvectors are scaled during the matrix transformation.
Definition of Eigenvalue
An eigenvalue is a scalar associated with a square matrix that quantifies the factor by which the eigenvector is scaled during a linear transformation. It satisfies the characteristic equation det(A - lI) = 0, where A is the matrix, l represents the eigenvalue, and I is the identity matrix. Unlike the determinant, which is a single scalar value representing the overall scaling factor of the transformation, eigenvalues provide detailed insights into the matrix's behavior along specific directions.
Mathematical Representation
The determinant of a matrix, denoted as det(A), is a scalar value representing the volume scaling factor and orientation change caused by the linear transformation defined by matrix A. Eigenvalues, denoted as l, satisfy the characteristic equation det(A - lI) = 0, where I is the identity matrix, linking eigenvalues directly to the determinant through this polynomial equation. The determinant itself equals the product of all eigenvalues of the matrix, expressing a fundamental connection between these two mathematical concepts.
Key Differences between Determinant and Eigenvalue
The determinant is a scalar value that indicates whether a square matrix is invertible, representing the product of all eigenvalues of the matrix. Eigenvalues are specific scalars associated with a matrix, revealing key properties such as the matrix's behavior under linear transformations and stability of systems. Unlike determinants, which provide a single summary measure, eigenvalues offer detailed insight into matrix structure through their individual values and multiplicities.
Importance in Linear Algebra
The determinant reveals key properties of a matrix, such as invertibility and volume scaling in linear transformations. Eigenvalues provide essential insights into the matrix's behavior by indicating characteristic roots that determine stability and long-term dynamics in systems. Both determinants and eigenvalues are fundamental in solving linear equations, performing matrix decompositions, and analyzing differential equations within linear algebra.
Applications of Determinants
Determinants play a crucial role in solving systems of linear equations, finding the invertibility of matrices, and calculating the volume scaling factor in linear transformations. They are widely used in engineering for stability analysis and in computer graphics for transformations and projections. Unlike eigenvalues that describe intrinsic properties of matrices related to their characteristic polynomial, determinants specifically indicate whether a matrix is singular or invertible, influencing various computational algorithms.
Applications of Eigenvalues
Eigenvalues play a critical role in diverse applications such as stability analysis in engineering, where they determine the behavior of dynamic systems and predict oscillations. In principal component analysis (PCA) for data science, eigenvalues help identify the most significant components by measuring variance explained in datasets. Quantum mechanics also relies on eigenvalues to determine measurable quantities like energy levels in physical systems.
Relationship between Determinant and Eigenvalues
The determinant of a square matrix equals the product of its eigenvalues, revealing a direct relationship between these two fundamental concepts in linear algebra. This relationship highlights that if any eigenvalue is zero, the determinant must also be zero, indicating the matrix is singular and non-invertible. Eigenvalues provide insight into the matrix's scaling effects on eigenvectors, while the determinant summarizes these effects into a single scalar value reflecting volume scaling.
Conclusion: Determinant vs Eigenvalue
The determinant of a matrix provides a single scalar value representing volume scaling and invertibility, while eigenvalues reveal intrinsic properties related to the matrix's linear transformations, such as stretching factors along specific directions. Determinants equal to zero indicate singular matrices, whereas eigenvalues include critical insights on stability and resonance in systems. Understanding both determinants and eigenvalues is essential for comprehensive matrix analysis in linear algebra and applied fields.
Determinant Infographic
 libterm.com
libterm.com