Primary education establishes the essential foundation for lifelong learning, fostering critical thinking and basic skills such as reading, writing, and arithmetic. It plays a crucial role in shaping social abilities, emotional development, and cognitive growth, preparing Your child for future academic success. Explore the rest of the article to understand how primary education impacts overall development and practical strategies to enhance learning outcomes.
Table of Comparison
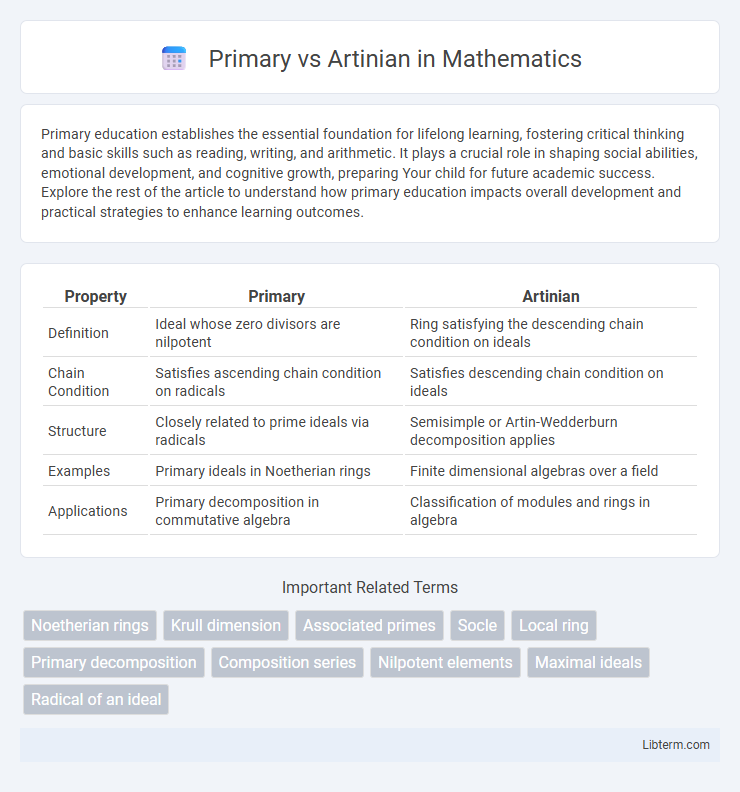
| Property | Primary | Artinian |
|---|---|---|
| Definition | Ideal whose zero divisors are nilpotent | Ring satisfying the descending chain condition on ideals |
| Chain Condition | Satisfies ascending chain condition on radicals | Satisfies descending chain condition on ideals |
| Structure | Closely related to prime ideals via radicals | Semisimple or Artin-Wedderburn decomposition applies |
| Examples | Primary ideals in Noetherian rings | Finite dimensional algebras over a field |
| Applications | Primary decomposition in commutative algebra | Classification of modules and rings in algebra |
Introduction to Primary and Artinian Concepts
Primary ideals in algebra are defined by the property that if a product ab belongs to the ideal and a is not in the ideal, then some power of b is in the ideal. Artinian rings or modules satisfy the descending chain condition on ideals or submodules, meaning no infinite strictly descending sequences exist. Understanding these foundational concepts is crucial for studying the structure and decomposition of rings in commutative algebra and module theory.
Definitions: Primary Modules and Artinian Modules
Primary modules are modules over a ring whose zero submodule has a primary annihilator, meaning the annihilator is a primary ideal that controls the module's structure through a single associated prime. Artinian modules satisfy the descending chain condition on submodules, ensuring every descending sequence of submodules stabilizes after finitely many steps. These definitions characterize primary modules via their annihilators linked to primary ideals, while Artinian modules are defined by their finiteness conditions on submodule chains.
Key Properties of Primary Modules
Primary modules are characterized by the property that every zero divisor is nilpotent on the module, ensuring a strong control over the annihilators of elements. In contrast, Artinian modules satisfy the descending chain condition on submodules, emphasizing finiteness conditions and stability of structure. The key property of primary modules lies in their close relationship to primary ideals, where the module structure reflects the behavior of powers of prime ideals in a ring.
Essential Characteristics of Artinian Modules
Artinian modules are characterized by the descending chain condition on submodules, ensuring every decreasing sequence of submodules stabilizes after finitely many steps. This property guarantees finite length and decomposability into simple modules, distinguishing Artinian modules from primary modules, which are defined by the behavior of their annihilators related to prime ideals. Essential characteristics of Artinian modules include their finite length, existence of minimal submodules, and the ability to reflect structural finiteness and decomposition uniquely via composition series.
Primary vs Artinian: Structural Differences
Primary rings have ideals whose every zero divisor is nilpotent, resulting in a unique minimal prime ideal that governs their structure. Artinian rings are characterized by satisfying the descending chain condition on ideals, leading to a decomposition into a finite product of Artinian local rings with simple module categories. The structural difference lies in primary rings emphasizing nilpotent behavior of zero divisors, while Artinian rings emphasize finite length and decomposition into semisimple components.
Examples of Primary and Artinian Modules
Primary modules include examples such as quotient modules of Noetherian rings modulo primary ideals, where the associated prime ideal controls the structure, like \( R/(p^n) \) for a prime ideal \( p \) and integer \( n \geq 1 \). Artinian modules arise typically in contexts where descending chain conditions hold, exemplified by finite-length modules over Artinian rings, such as simple modules over a field or the additive group of integers modulo \( n \). These examples illustrate the distinction: primary modules generalize the concept of primary decomposition in commutative algebra, while Artinian modules emphasize finiteness conditions related to chain conditions on submodules.
Relationships and Hierarchies between Primary and Artinian
Primary ideals represent a generalization of prime ideals where every zero divisor within the quotient ring is nilpotent, while Artinian rings are defined by the descending chain condition on ideals ensuring finite length. The hierarchy places Artinian rings as a subclass of Noetherian rings, often decomposable into finite intersections of primary components corresponding to primary ideals. Relationships between primary and Artinian structures emerge in the primary decomposition theorem, where Artinian rings facilitate decompositions into primary ideals reflecting the ring's hierarchical structure.
Applications in Commutative Algebra
Primary ideals play a crucial role in decomposing modules and ring elements into simpler components, facilitating the analysis of algebraic structures in commutative algebra. Artinian rings, characterized by descending chain conditions on ideals, are essential in local algebra and representation theory due to their finite length modules and rich structural properties. Applications in algebraic geometry and invariant theory leverage primary decomposition and Artinian properties to study singularities, multiplicities, and module behaviors over Noetherian rings.
Common Theorems Involving Primary and Artinian
Primary and Artinian modules are central in algebraic theory, with key theorems such as the Primary Decomposition Theorem stating that any submodule of a module over a Noetherian ring can be expressed as an intersection of finitely many primary submodules. The Artin-Rees Lemma provides a crucial link between primary ideals and Artinian modules, ensuring control over filtrations in Noetherian settings. Moreover, the characterization that every Artinian module has finite length, while primary modules generalize the concept of nilpotent elements, highlights their intertwined roles in ring and module theory.
Summary and Final Comparison
Primary ideals in ring theory are closely related to the decomposition of ideals into simpler components, characterized by having their zero divisors contained within a single prime ideal. Artinian rings, defined by the descending chain condition on ideals, exhibit finiteness properties that guarantee a well-structured and finite composition series. The final comparison highlights that while primary decomposition focuses on ideal structure in general rings, Artinian rings provide a more rigid framework ensuring ideals stabilize quickly, making their module theory and classification significantly more manageable.
Primary Infographic
 libterm.com
libterm.com