A disk is a versatile storage device essential for saving and retrieving digital data efficiently. Its structure and technology impact your system's speed, capacity, and reliability. Explore the rest of the article to understand how different types of disks can enhance your computing experience.
Table of Comparison
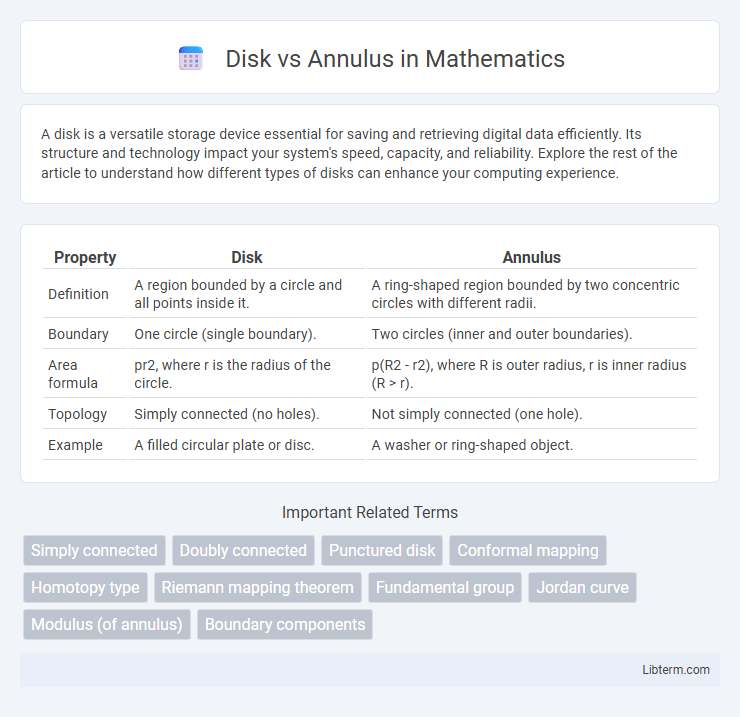
| Property | Disk | Annulus |
|---|---|---|
| Definition | A region bounded by a circle and all points inside it. | A ring-shaped region bounded by two concentric circles with different radii. |
| Boundary | One circle (single boundary). | Two circles (inner and outer boundaries). |
| Area formula | pr2, where r is the radius of the circle. | p(R2 - r2), where R is outer radius, r is inner radius (R > r). |
| Topology | Simply connected (no holes). | Not simply connected (one hole). |
| Example | A filled circular plate or disc. | A washer or ring-shaped object. |
Introduction to Disk and Annulus
A disk in geometry is the region in a plane enclosed by a circle, including all points inside the circle's boundary, defined by a fixed radius from a central point. An annulus, by contrast, is the area bounded by two concentric circles with different radii, representing the difference between two disks. Understanding disks and annuli establishes foundational concepts for studying planar regions and their properties in Euclidean geometry.
Definitions: What is a Disk?
A disk is a two-dimensional geometric shape consisting of all points in a plane that lie within a fixed distance, called the radius, from a central point. It includes both the boundary circle and the interior area enclosed by that circle. In mathematical terms, a disk is defined as the set of points \((x, y)\) such that \(\sqrt{(x - h)^2 + (y - k)^2} \leq r\), where \((h, k)\) is the center and \(r\) is the radius.
Definitions: What is an Annulus?
An annulus is a geometric shape defined as the region bounded by two concentric circles with different radii, forming a ring-like area. Unlike a disk, which includes all points within a single circle, an annulus excludes the inner circle's interior, creating a hollow space in the center. This distinction is crucial in fields such as mathematics and engineering where precise area calculations and properties are required.
Mathematical Properties and Formulas
A disk is a two-dimensional shape consisting of all points in a plane within a fixed radius \(r\) from a center point, characterized by the formula for area \(A = \pi r^2\) and circumference \(C = 2\pi r\). An annulus is a ring-shaped region bounded by two concentric circles with radii \(r_1\) and \(r_2\) (\(r_2 > r_1\)), where the area is given by \(A = \pi (r_2^2 - r_1^2)\) and the perimeter equals the sum of the circumferences of both circles, \(P = 2\pi (r_1 + r_2)\). Both shapes demonstrate fundamental properties in planar geometry used in fields such as calculus, complex analysis, and electromagnetic theory.
Visual Representation and Geometry
A disk is a filled circular region defined by all points within a certain radius from a center point, representing a solid shape in geometry. An annulus consists of the area between two concentric circles with different radii, resembling a ring or hollow circle. Visually, a disk appears as a solid circle, while an annulus looks like a circular band with an empty center.
Key Differences: Disk vs Annulus
A disk is a two-dimensional geometric shape consisting of all points within a fixed radius from a center point, forming a solid circular area, while an annulus is a ring-shaped region bounded by two concentric circles with different radii, creating a hollow circular area. The key difference lies in the presence of an inner boundary in an annulus, which the disk lacks, making the annulus a shape with a hole in the center. In mathematical analysis, disks are often used to represent simple circular regions, whereas annuli model more complex structures involving inner voids or rings.
Applications in Mathematics and Physics
Disks and annuli serve crucial roles in mathematics and physics, particularly in complex analysis, potential theory, and fluid dynamics. Disks are often used to define regions for conformal mappings and are fundamental in solving boundary value problems involving Laplace's equation. Annuli model ring-shaped domains essential for studying phenomena such as heat transfer in cylindrical shells and electromagnetic fields around coaxial cables.
Disk and Annulus in Real-World Contexts
Disks and annuli frequently appear in engineering and natural sciences, where disks often represent circular areas like gears or lenses, providing foundational shapes for mechanical and optical devices. Annuli, characterized by their ring-like shape with an inner and outer radius, model phenomena such as heat distribution in pipe cross-sections or stress analysis in rotating machinery parts. Understanding the specific properties of disks and annuli enables precise calculations in material science, fluid dynamics, and architectural design, enhancing efficiency and safety in practical applications.
Advantages and Limitations of Each Shape
A disk shape provides uniform radial symmetry, enabling efficient stress distribution and simplified manufacturing for mechanical components such as brake rotors and optical lenses, but its limited surface area restricts heat dissipation and mounting options. An annulus offers enhanced cooling capabilities and reduced weight due to the central hole, making it ideal for applications like turbines and sealed bearings, yet it introduces complexity in stress concentration and potential structural weaknesses near the inner diameter. Optimal selection between disk and annulus depends on balancing mechanical performance, thermal management, and application-specific constraints.
Conclusion: Choosing Between Disk and Annulus
Choosing between a disk and an annulus depends primarily on the spatial domain and boundary conditions of the problem at hand. Disks are ideal for scenarios requiring analysis within a compact, simply connected circular area, while annuli are suited for problems involving ring-shaped regions with inner and outer boundaries. The decision hinges on the geometric characteristics influencing integral calculations, eigenvalue problems, and potential theory applications.
Disk Infographic
 libterm.com
libterm.com