A symplectic manifold is a smooth, even-dimensional space equipped with a closed, non-degenerate 2-form called the symplectic form, crucial for the mathematical framework of classical mechanics. This structure enables the study of geometric properties of phase space and Hamiltonian dynamics. Explore the rest of the article to deepen your understanding of symplectic manifolds and their applications.
Table of Comparison
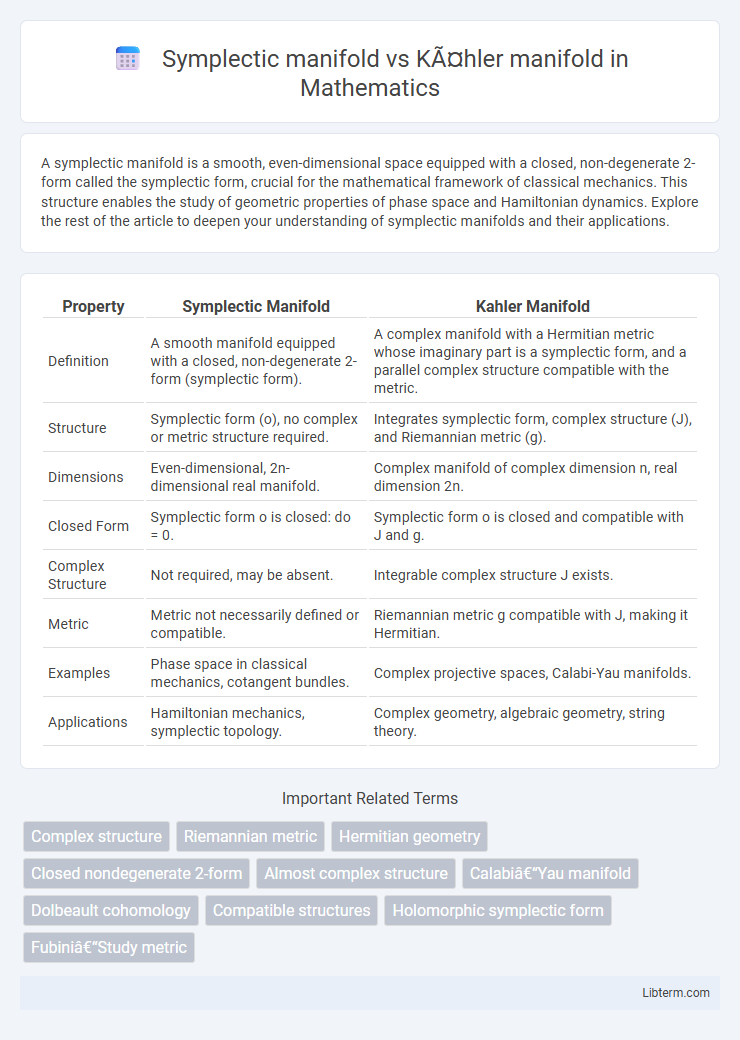
| Property | Symplectic Manifold | Kahler Manifold |
|---|---|---|
| Definition | A smooth manifold equipped with a closed, non-degenerate 2-form (symplectic form). | A complex manifold with a Hermitian metric whose imaginary part is a symplectic form, and a parallel complex structure compatible with the metric. |
| Structure | Symplectic form (o), no complex or metric structure required. | Integrates symplectic form, complex structure (J), and Riemannian metric (g). |
| Dimensions | Even-dimensional, 2n-dimensional real manifold. | Complex manifold of complex dimension n, real dimension 2n. |
| Closed Form | Symplectic form o is closed: do = 0. | Symplectic form o is closed and compatible with J and g. |
| Complex Structure | Not required, may be absent. | Integrable complex structure J exists. |
| Metric | Metric not necessarily defined or compatible. | Riemannian metric g compatible with J, making it Hermitian. |
| Examples | Phase space in classical mechanics, cotangent bundles. | Complex projective spaces, Calabi-Yau manifolds. |
| Applications | Hamiltonian mechanics, symplectic topology. | Complex geometry, algebraic geometry, string theory. |
Introduction to Symplectic and Kähler Manifolds
Symplectic manifolds are smooth even-dimensional spaces equipped with a closed, non-degenerate 2-form called the symplectic form, which provides a framework for classical mechanics and Hamiltonian dynamics. Kahler manifolds are complex manifolds endowed with a Hermitian metric whose imaginary part defines a symplectic form compatible with the complex structure, integrating symplectic, complex, and Riemannian geometry. The interplay between the symplectic form, complex structure, and metric in Kahler manifolds leads to rich geometric properties absent in general symplectic manifolds.
Defining Symplectic Manifolds: Key Properties
Symplectic manifolds are smooth, even-dimensional spaces equipped with a closed, non-degenerate 2-form called the symplectic form, which provides a geometric framework for classical mechanics and Hamiltonian dynamics. This 2-form, o, satisfies do = 0 and o^n 0 at each point, ensuring volume preservation and orientation in 2n-dimensional manifolds. Unlike Kahler manifolds, which require an integrable complex structure compatible with a Hermitian metric, symplectic manifolds do not necessitate complex or metric structures, highlighting their broader application in differential geometry.
Understanding Kähler Manifolds: Essential Features
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose imaginary part defines a symplectic form, creating a rich structure combining complex, symplectic, and Riemannian geometry. The essential features of Kahler manifolds include the closedness of the Kahler form, integrability of the complex structure, and compatibility between the metric and symplectic form, ensuring harmonic forms and Hodge theory apply. Unlike general symplectic manifolds, Kahler manifolds support a complex structure that is parallel with respect to the Levi-Civita connection, resulting in powerful geometric and topological properties.
Structural Differences: Symplectic vs Kähler Manifolds
Symplectic manifolds are smooth even-dimensional manifolds equipped with a closed, non-degenerate 2-form called the symplectic form, which provides a framework for Hamiltonian mechanics without requiring an integrable complex structure. Kahler manifolds, on the other hand, are a special class of complex manifolds endowed with a Hermitian metric whose associated (1,1)-form is both closed and symplectic, resulting in a rich interplay between complex, symplectic, and Riemannian geometry. The structural difference hinges on integrability and compatibility conditions: Kahler manifolds require an integrable complex structure and a compatible Riemannian metric, while symplectic manifolds need only a non-degenerate closed 2-form, allowing more general geometric configurations.
Relationship with Complex Geometry
Symplectic manifolds provide a general framework for geometry defined by a closed, non-degenerate 2-form, while Kahler manifolds represent a special class that intertwines symplectic, complex, and Riemannian geometries through a compatible triple structure. The Kahler condition imposes integrability on the complex structure, making Kahler manifolds both complex manifolds and symplectic manifolds with a compatible Hermitian metric. This relationship highlights the role of Kahler manifolds in complex geometry as spaces where symplectic and complex structures coexist harmoniously, enabling rich geometric and topological applications such as Hodge theory and mirror symmetry.
Compatibility of Metrics and Forms
Symplectic manifolds possess a closed, non-degenerate 2-form called the symplectic form, which does not inherently define a compatible metric. Kahler manifolds integrate a symplectic form, a complex structure, and a Riemannian metric that satisfy compatibility conditions, ensuring the metric is Hermitian and the symplectic form is Kahler, meaning it is closed and compatible with both structures. This compatibility makes Kahler manifolds a special subclass of symplectic manifolds with additional geometric and analytic properties due to the interplay of metric, form, and complex structure.
Examples of Symplectic Manifolds
Symplectic manifolds include classical phase spaces like the cotangent bundle of a smooth manifold and the even-dimensional Euclidean space equipped with the standard symplectic form. A Kahler manifold is a complex manifold with a compatible symplectic form and Riemannian metric, such as complex projective spaces and complex tori. Unlike Kahler manifolds, symplectic manifolds need not have an integrable complex structure, allowing for a broader class including aspherical symplectic 4-manifolds and certain toric varieties.
Examples of Kähler Manifolds
Kahler manifolds are a special class of symplectic manifolds equipped with a compatible complex structure and a Riemannian metric, making them rich geometric objects. Prominent examples include complex projective spaces CP^n, which carry the Fubini-Study metric, and smooth complex algebraic varieties such as complex tori and Calabi-Yau manifolds. These examples showcase the interplay between symplectic forms, complex structures, and metrics that satisfy the Kahler condition, distinguishing Kahler manifolds within the broader category of symplectic manifolds.
Applications in Mathematics and Physics
Symplectic manifolds provide the mathematical framework for classical mechanics, particularly in Hamiltonian systems where they model phase spaces with a non-degenerate closed 2-form. Kahler manifolds, combining symplectic, complex, and Riemannian structures, are essential in algebraic geometry and string theory, enabling the study of complex differential equations and mirror symmetry. Their interplay facilitates advances in quantization, geometric representation theory, and supersymmetric field theories in mathematical physics.
Choosing Between Symplectic and Kähler Manifolds
Choosing between symplectic and Kahler manifolds depends on the geometric structures and applications involved: symplectic manifolds emphasize a non-degenerate, closed 2-form ideal for Hamiltonian mechanics and classical dynamics, while Kahler manifolds integrate a compatible complex structure, symplectic form, and Riemannian metric, crucial for complex differential geometry and algebraic geometry. Researchers prioritize symplectic manifolds when studying purely symplectic phenomena without the necessity for a complex structure, whereas Kahler manifolds are preferred for problems requiring rich interactions between complex geometry, metric properties, and symplectic forms. The decision impacts both theoretical frameworks and practical computations in fields such as mathematical physics, string theory, and complex manifold theory.
Symplectic manifold Infographic
 libterm.com
libterm.com