A partial function is a type of function that is not defined for every possible input value in its domain, meaning it may only work for a subset of inputs. Unlike total functions, partial functions can yield results for specific inputs while being undefined or invalid for others, which is essential to understand in computer science and mathematics. Explore the rest of this article to learn how partial functions impact programming and problem-solving in your projects.
Table of Comparison
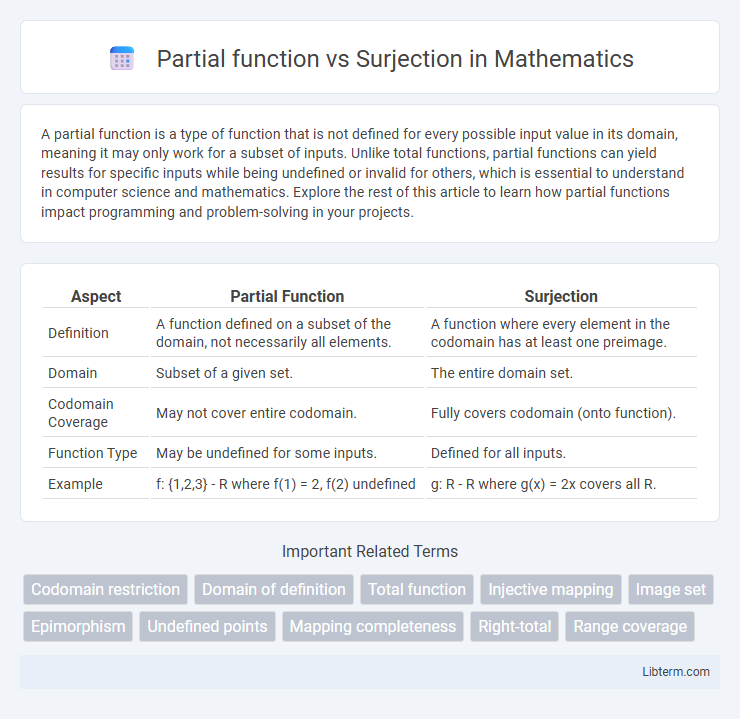
| Aspect | Partial Function | Surjection |
|---|---|---|
| Definition | A function defined on a subset of the domain, not necessarily all elements. | A function where every element in the codomain has at least one preimage. |
| Domain | Subset of a given set. | The entire domain set. |
| Codomain Coverage | May not cover entire codomain. | Fully covers codomain (onto function). |
| Function Type | May be undefined for some inputs. | Defined for all inputs. |
| Example | f: {1,2,3} - R where f(1) = 2, f(2) undefined | g: R - R where g(x) = 2x covers all R. |
Introduction to Partial Functions and Surjections
Partial functions are mappings from a subset of a domain to a codomain, meaning they may not provide an output for every element in the domain. Surjections, or onto functions, guarantee every element in the codomain is mapped by at least one element of the entire domain, ensuring coverage without exceptions. Understanding the distinction between partial functions and surjections is fundamental in fields like mathematics and computer science, where domain completeness and codomain reachability are key concepts.
Defining Partial Functions
Partial functions are mathematical mappings from a subset of a domain to a codomain, differing from surjections which require every element in the codomain to be mapped by at least one element in the domain. Defining partial functions involves specifying the domain subset on which the function is defined, allowing undefined values outside this subset. Surjections, or onto functions, are total functions where the function's image equals the entire codomain, contrasting the partial function's potentially incomplete mapping.
Understanding Surjective (Onto) Functions
Surjective functions, also known as onto functions, ensure every element in the codomain has at least one preimage in the domain, creating a complete mapping. In contrast, partial functions may not provide outputs for every input in the domain, leading to undefined values. Understanding surjections is crucial for analyzing function properties in set theory and computing, as they guarantee full coverage of the codomain.
Key Differences Between Partial Functions and Surjections
Partial functions are mappings from a subset of a domain to a codomain, meaning they may be undefined for some elements of the domain, while surjections are functions where every element of the codomain has at least one preimage in the domain. The key difference lies in totality; surjections are total functions with complete domain coverage, whereas partial functions allow incomplete domain assignment. Surjections guarantee onto mapping, ensuring every output is hit, whereas partial functions do not require the codomain to be fully mapped.
Domain and Codomain Considerations
A partial function is defined on a subset of its domain, meaning it does not assign an output to every element in the domain, whereas a surjection (onto function) maps every element of its codomain to at least one element of its domain. In domain and codomain considerations, a partial function's domain is typically smaller or restricted compared to a surjection, which requires a complete domain to ensure every codomain element has a preimage. The surjection guarantees full codomain coverage, while the partial function may leave parts of the domain undefined, impacting how these functions are applied in mathematical analysis and computer science.
Examples of Partial Functions
Partial functions differ from surjections in that partial functions may be undefined for some inputs within their domain, whereas surjections map every element of the domain onto the entire codomain. For example, the square root function defined only for non-negative real numbers is a partial function from the real numbers to itself, as it lacks output for negative inputs. Another example is the natural logarithm function, which is a partial function from positive real numbers to real numbers, undefined for non-positive values, contrasting with surjective functions that cover their codomain completely.
Examples of Surjection
Surjection, or onto function, maps every element of the codomain to at least one element of the domain, ensuring complete coverage of the codomain. An example of a surjection is the function f(x) = 2x from the set of all integers to the set of even integers, where every even integer has a preimage. Partial functions differ by being undefined for some inputs, whereas surjections are total functions with fully mapped codomains.
Practical Applications and Use Cases
Partial functions are essential in computer science for modeling computations that may not return a value for every input, such as error handling in programming languages and database queries where data may be incomplete. Surjections, or onto functions, guarantee every element in the codomain is mapped, making them crucial in data encoding, hashing algorithms, and ensuring coverage in classification problems. Understanding the distinction aids in designing robust software systems, optimizing resource allocation, and improving data transformation processes.
Visual Representation and Mapping
Partial functions map elements from a subset of the domain to the codomain, resulting in some domain elements without an assigned image, often illustrated by arrows missing from certain domain points. Surjections (onto functions) cover every element in the codomain at least once, depicted with arrows from the entire domain reaching all codomain elements. Visual representations highlight these differences by showing partial functions with incomplete arrows and surjections with full codomain coverage, emphasizing the completeness of mapping in surjections versus the selective mapping in partial functions.
Summary: Partial Function vs Surjection
A partial function maps elements from a domain to a codomain where some inputs may have no output, while a surjection is a total function that covers every element in the codomain at least once. In a surjection, every value in the codomain is an image of at least one input from the domain, ensuring complete coverage. Partial functions may be undefined for certain inputs, lacking the surjective property of mapping onto the entire codomain.
Partial function Infographic
 libterm.com
libterm.com