A power series is an infinite sum of terms in the form \(a_n (x - c)^n\), where \(a_n\) represents coefficients and \(c\) is the center of the series. Understanding the radius and interval of convergence is essential for determining where the series accurately represents a function. Explore the rest of the article to deepen your knowledge of power series applications and convergence tests.
Table of Comparison
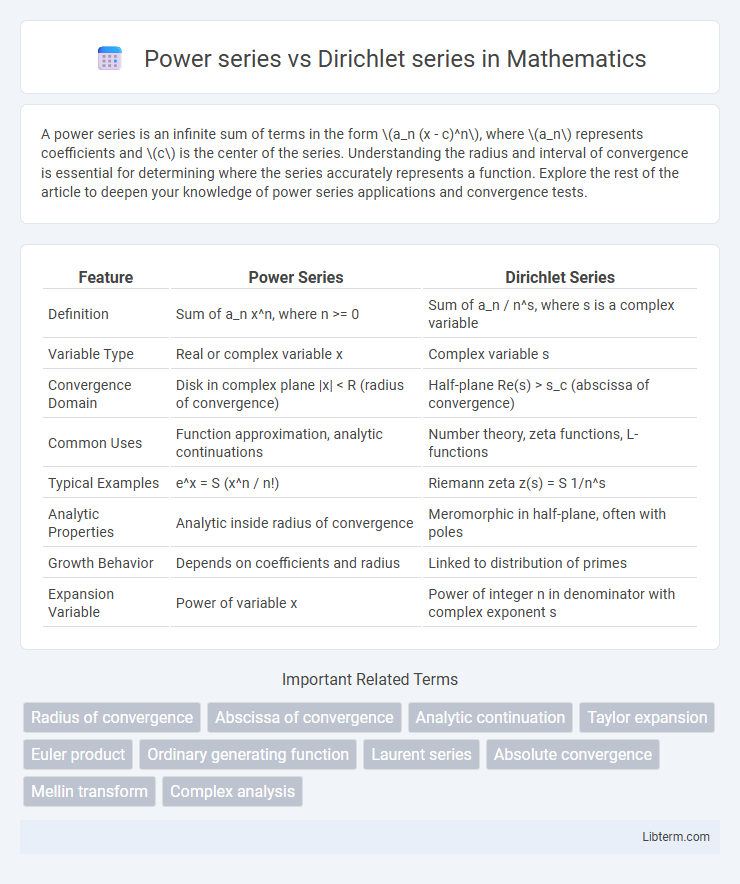
| Feature | Power Series | Dirichlet Series |
|---|---|---|
| Definition | Sum of a_n x^n, where n >= 0 | Sum of a_n / n^s, where s is a complex variable |
| Variable Type | Real or complex variable x | Complex variable s |
| Convergence Domain | Disk in complex plane |x| < R (radius of convergence) | Half-plane Re(s) > s_c (abscissa of convergence) |
| Common Uses | Function approximation, analytic continuations | Number theory, zeta functions, L-functions |
| Typical Examples | e^x = S (x^n / n!) | Riemann zeta z(s) = S 1/n^s |
| Analytic Properties | Analytic inside radius of convergence | Meromorphic in half-plane, often with poles |
| Growth Behavior | Depends on coefficients and radius | Linked to distribution of primes |
| Expansion Variable | Power of variable x | Power of integer n in denominator with complex exponent s |
Introduction to Power Series and Dirichlet Series
Power series are infinite sums of the form anxn where coefficients an depend on natural numbers and converge within a radius determined by the variable x. Dirichlet series, expressed as an/ns, involve complex variables s and coefficients an indexed by natural numbers, commonly used in analytic number theory. Both series types analyze functions through infinite expansions but differ fundamentally in variable domains and convergence properties.
Fundamental Definitions and Concepts
A power series is an infinite series of the form \(\sum_{n=0}^{\infty} a_n (x - c)^n\), where \(a_n\) are coefficients and \(c\) is the center of expansion, primarily used to represent analytic functions within a radius of convergence. A Dirichlet series is expressed as \(\sum_{n=1}^{\infty} \frac{a_n}{n^s}\), with complex variable \(s\) and coefficients \(a_n\), widely employed in number theory and complex analysis to study arithmetic functions and L-functions. The fundamental difference lies in the variable dependence and convergence domain: power series converge within discs in the complex plane, whereas Dirichlet series converge in half-planes defined by the real part of \(s\).
Convergence Criteria: Power Series vs Dirichlet Series
Power series converge based on the radius of convergence determined by the distance from the center to the nearest singularity, typically evaluated using the root or ratio test. Dirichlet series convergence depends on the real part of the complex variable, with absolute convergence occurring in half-planes where the real part exceeds a critical abscissa known as the abscissa of absolute convergence. The fundamental difference lies in power series having circular regions of convergence, while Dirichlet series converge in right half-planes defined by vertical lines in the complex plane.
Algebraic Structure and Operations
Power series and Dirichlet series differ fundamentally in their algebraic structures and operations. Power series form a commutative algebra under formal addition and convolution-like multiplication, where coefficients correspond to powers of a single variable, enabling operations such as differentiation and integration within the ring of formal power series. Dirichlet series, associated with arithmetic functions, possess a multiplicative structure under Dirichlet convolution and naturally encode number-theoretic information, making their algebraic operations closely tied to the properties of integers and prime factorization.
Analytic Properties and Domains of Convergence
Power series converge within a radius determined by the distance to the nearest singularity on the complex plane, exhibiting analytic properties characterized by holomorphic functions inside this disk. Dirichlet series converge in half-planes defined by the real part of the complex variable exceeding a specific abscissa of convergence and often extend meromorphically beyond this domain through analytic continuation. The analytic structure of power series is local and centered around a point, while Dirichlet series capture global analytic behavior linked to number-theoretic functions across vertical strips in the complex plane.
Applications in Mathematical Analysis
Power series are widely used in mathematical analysis for solving differential equations, approximating functions, and studying convergence properties within complex analysis. Dirichlet series find significant applications in number theory, particularly in analytic continuation and the study of L-functions and the distribution of prime numbers. Both series types serve as fundamental tools in spectral theory and harmonic analysis, enabling deeper insights into functional spaces and arithmetic functions.
Role in Complex Analysis and Number Theory
Power series play a fundamental role in complex analysis by representing holomorphic functions as infinite sums, enabling analytic continuation and local behavior study near singularities. Dirichlet series are central in number theory, particularly in encoding arithmetic functions and studying properties of prime numbers through analytic methods, such as in the theory of L-functions and the Riemann zeta function. Both series types bridge complex analysis and number theory by linking analytical properties with arithmetic structures, but power series focus on function theory in complex domains while Dirichlet series emphasize multiplicative number-theoretic information.
Key Differences and Similarities
Power series and Dirichlet series both serve as infinite series representations of functions but differ fundamentally in their structure and applications. Power series take the form \(\sum_{n=0}^\infty a_n z^n\), relying on integer powers of a complex variable \(z\), while Dirichlet series are expressed as \(\sum_{n=1}^\infty \frac{a_n}{n^s}\), involving terms with reciprocals of integers raised to a complex exponent \(s\). Convergence regions for power series depend on the radius in the complex plane, whereas Dirichlet series convergence hinges on the real part of \(s\), reflecting their respective roles in analytic functions and number theory.
Examples and Illustrative Calculations
Power series such as _{n=0}^ a_n x^n exemplify expansions around a point, with geometric series _{n=0}^ x^n = 1/(1-x) for |x|<1 as a fundamental example, used in analytic function approximations. Dirichlet series, exemplified by the Riemann zeta function z(s) = _{n=1}^ 1/n^s for Re(s) > 1, appear in number theory and encode prime distributions through Euler products. Illustrative calculations show power series convergence relates to radius in the complex plane, whereas Dirichlet series convergence depends on the real part of s, distinguishing their analytic and arithmetic applications.
Conclusion and Further Directions
Power series provide highly effective tools for analytic functions near finite points, characterized by simpler convergence criteria and extensive applications in calculus and complex analysis. Dirichlet series, often employed in number theory and complex variables, exhibit intricate convergence domains linked to the distribution of coefficients, offering unique insights into prime numbers and L-functions. Future research may explore hybrid approaches combining power and Dirichlet series to advance understanding of analytic continuation, zero distribution, and applications in modern analytic number theory.
Power series Infographic
 libterm.com
libterm.com