Exterior algebra provides a powerful framework for studying geometric and algebraic structures through the use of antisymmetric tensors and wedge products. It plays a crucial role in differential geometry, physics, and computer science by enabling the manipulation of multidimensional volumes and orientations. Explore the rest of the article to discover how exterior algebra can enhance your understanding of complex mathematical systems.
Table of Comparison
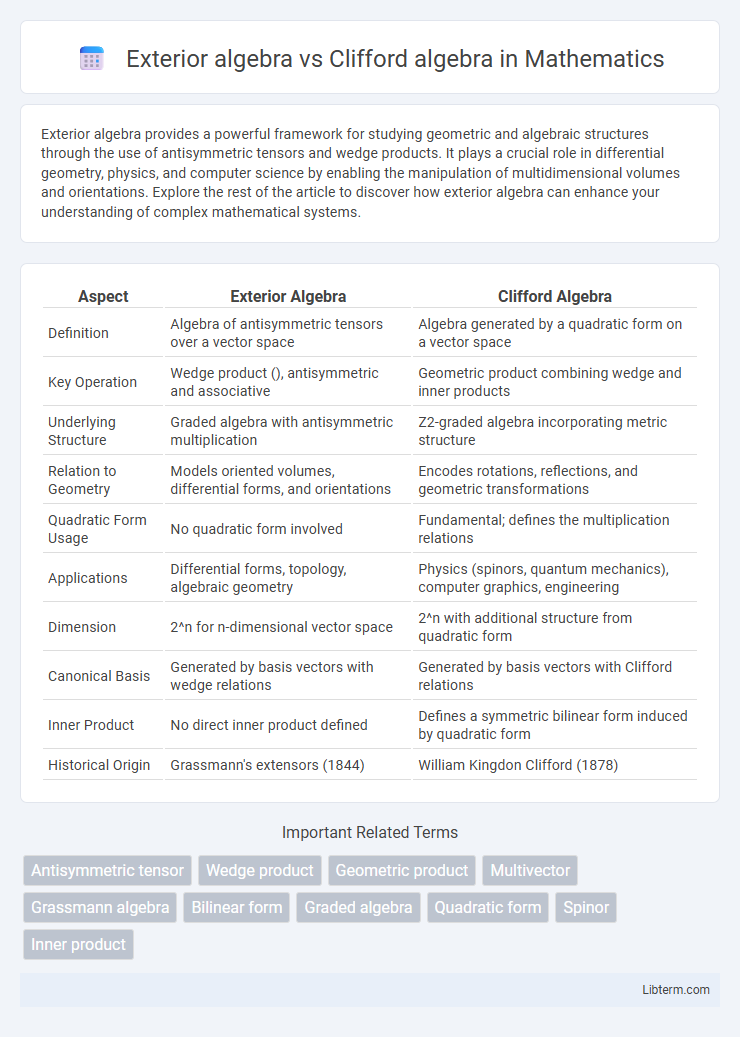
| Aspect | Exterior Algebra | Clifford Algebra |
|---|---|---|
| Definition | Algebra of antisymmetric tensors over a vector space | Algebra generated by a quadratic form on a vector space |
| Key Operation | Wedge product (), antisymmetric and associative | Geometric product combining wedge and inner products |
| Underlying Structure | Graded algebra with antisymmetric multiplication | Z2-graded algebra incorporating metric structure |
| Relation to Geometry | Models oriented volumes, differential forms, and orientations | Encodes rotations, reflections, and geometric transformations |
| Quadratic Form Usage | No quadratic form involved | Fundamental; defines the multiplication relations |
| Applications | Differential forms, topology, algebraic geometry | Physics (spinors, quantum mechanics), computer graphics, engineering |
| Dimension | 2^n for n-dimensional vector space | 2^n with additional structure from quadratic form |
| Canonical Basis | Generated by basis vectors with wedge relations | Generated by basis vectors with Clifford relations |
| Inner Product | No direct inner product defined | Defines a symmetric bilinear form induced by quadratic form |
| Historical Origin | Grassmann's extensors (1844) | William Kingdon Clifford (1878) |
Introduction to Exterior Algebra and Clifford Algebra
Exterior algebra constructs multivectors using wedge products, emphasizing antisymmetric combinations of vectors ideal for areas like differential geometry and multilinear algebra. Clifford algebra extends exterior algebra by incorporating a quadratic form, enabling the definition of a geometric product that combines both symmetric and antisymmetric components, which is crucial in physics and computer graphics for encoding rotations and reflections. The foundational difference lies in how Clifford algebra generalizes exterior algebra's antisymmetric wedge product to include metric-dependent operations, enriching its algebraic structure and applications.
Fundamental Concepts and Definitions
Exterior algebra is a mathematical framework centered on the wedge product, constructing antisymmetric tensors that model oriented volumes in vector spaces. Clifford algebra extends exterior algebra by incorporating a quadratic form, enabling the combination of the wedge product with geometric multiplication to represent rotations and reflections in various dimensions. Key definitions include multivectors in exterior algebra versus the Clifford product in Clifford algebra, where the latter captures both the antisymmetric and symmetric parts of vector multiplication.
Historical Background and Development
Exterior algebra, introduced by Hermann Grassmann in the mid-19th century, laid the foundation for multilinear algebra through its development of the wedge product to represent oriented volumes. Clifford algebra, formulated by William Kingdon Clifford in the late 19th century, extended Grassmann's exterior algebra by incorporating a quadratic form, enabling the algebraic treatment of geometric transformations and rotations. This evolution from exterior to Clifford algebra marked a pivotal advancement in both mathematical theory and applications, influencing fields such as differential geometry and theoretical physics.
Structure and Operations in Exterior Algebra
Exterior algebra is built on antisymmetric wedge products of vectors, forming multivectors that represent oriented subspaces. Its structure emphasizes graded components, where the wedge product of k-vectors yields (k+l)-vectors, maintaining antisymmetry and multilinearity. Operations in exterior algebra include the wedge product, exterior derivative, and Hodge star, enabling manipulation of differential forms and encoding geometric information without relying on a metric.
Structure and Operations in Clifford Algebra
Clifford algebra extends exterior algebra by incorporating a bilinear form that defines a geometric product, combining antisymmetric wedge products with symmetric inner products. Its structure includes multivectors with grades that interact through this product, enabling representations of rotations and reflections beyond the purely antisymmetric operations of exterior algebra. Operations in Clifford algebra facilitate the encoding of geometric transformations and metric information, making it a powerful framework in physics and computer graphics.
Key Differences between Exterior and Clifford Algebras
Exterior algebra primarily deals with antisymmetric wedge products of vectors, forming a graded algebra that encodes oriented subspaces and areas. Clifford algebra extends exterior algebra by incorporating a quadratic form, allowing the definition of a geometric product that combines both inner and outer products, enabling the algebraic representation of rotations and reflections. The key difference lies in Clifford algebra's ability to model metric properties and geometric transformations, whereas exterior algebra focuses on orientation and volume without explicit metric structure.
Geometric Interpretations and Applications
Exterior algebra provides a framework for representing oriented subspaces and calculating volumes using wedge products, which makes it essential in differential geometry and multilinear algebra. Clifford algebra extends exterior algebra by incorporating a geometric product that combines both inner and outer products, enabling the representation of rotations, reflections, and complex transformations in Euclidean and pseudo-Euclidean spaces. This enhanced geometric interpretation allows Clifford algebra to be widely applied in physics, computer graphics, robotics, and quantum mechanics for modeling spacetime, spinors, and geometric transformations.
Role in Physics and Engineering
Exterior algebra provides a foundation for differential geometry and is widely used in physics and engineering to describe oriented volumes, flux, and integration on manifolds through wedge products. Clifford algebra extends exterior algebra by incorporating a geometric product that combines the inner and outer products, enabling concise representation of rotations, reflections, and spacetime transformations crucial in quantum mechanics, relativity, and robotics. Its ability to model geometric transformations and multivector fields makes Clifford algebra a powerful tool for solving complex physical problems and engineering designs involving spatial reasoning and signal processing.
Computational Aspects and Algorithmic Use
Exterior algebra simplifies computations by representing multi-dimensional oriented volumes using wedge products, facilitating straightforward antisymmetric operations in geometric modeling and differential geometry. Clifford algebra extends this framework by integrating a metric through the geometric product, enabling efficient encoding of rotations, reflections, and other transformations essential in computer graphics and robotics. Algorithmically, Clifford algebra supports more versatile and compact computations involving both geometric objects and transformations, often reducing complexity compared to purely exterior algebra-based approaches.
Choosing between Exterior and Clifford Algebra for Problem Solving
Choosing between exterior algebra and Clifford algebra depends on the nature of the problem and the desired algebraic properties. Exterior algebra excels in handling oriented volume elements and antisymmetric relationships, making it ideal for differential forms and multivector calculations in geometry. Clifford algebra extends exterior algebra by incorporating a geometric product, enabling unified treatment of rotations, reflections, and metric-dependent operations crucial for physics and computer graphics.
Exterior algebra Infographic
 libterm.com
libterm.com